Chalk & Talk Podcast Notes – Anna Stokke

Olivier Chabot|September 8, 2023|Learning, Mathematics, Notes, Podcast Notes, Studying, Teaching
Reading Time: 7 minutes
Post Views: 465

Here are my notes for Anna Stokke’s Chalk & Talk podcast. I’d highly recommend the podcast if you’re a math teacher. I’ll do my best to update this article as I listen to future episodes.

Favourite Episodes

Below are my personal notes taken using the Snipd podcast app.

Takeaways

Explicit Instruction

  • Explicit Instruction works. Please don’t feel bad about it. Do modelling (explaining your thinking) and worked examples. Scaffold your way up. Remove these scaffolds slowly as they gain proficiency.
  • Explicit instruction is the most interactive form of instruction (Zach Groshell hot take). Ask students tons of questions and ask them to show their answers on mini-whiteboards or circulate the classroom to verify their understanding (Ep. 6). At my school, students are allowed to write on their desks with a dry-erase marker. I often write on their desk as I circulate to give them hints or make them think about something.
  • Ways to check for understanding:
    • Mini-whiteboards / write on desks / write on worksheet (minimize social judgment – Dan Rosen)
    • Finger voting
    • Raise your hand if you know the answer
    • Raise your hand if you agree with this answer
    • Current comfort level: 1 (lost) to 5 (too easy) finger vote
    • Cold calling (given a mistake-friendly culture – Dan Rosen)
    • Turn and talk
    • Think-Pair-Share (Pense-Parle-Partage)
  • High-Impact Instructional Practices in Mathematics in Ontario
  • “Explicitly teaching kids how to do things works” (Matthew Burns). I’m not sure why that is a hot take when you think about it.
  • Discovery-based learning is not how you want to introduce new concepts. It overwhelms the students with low proficiency and contributes to their ingrained belief that they can’t do math (Robin Codding). You’re the expert. Own it. Give them the gift of mastery (Tom Bennett).
    • Low floor, high ceiling problems are great, but why not scaffold everybody to the ceiling and ensure mastery? (Tom Bennett)
  • Learning doesn’t need to be fun. One of the most reliable ways to get kids to like math is to make sure they’re able to do the exercises. In short, competence leads to liking math way more than the other way around. (Greg Ashman)
  • The job of the instructor is to make learning as easy as possible through careful scaffolding. The idea that intense struggle leads to deeper learning is overrated, if not wrong altogether (Greg Ashman & Matthew Burns). Making learning as easy as possible is one of the most compassionate things you can do for your students (Zach Groshell).
  • Start each lesson with verbal retrieval of big ideas and homework problems (Patrice Bain).
  • Teach students the algorithms and explain why it works. The priority is that students can use and apply the technique first and foremost. Comprehension is bound to come eventually (Ep. 17). Why do we care so much about understanding? What does understanding even mean? I’m not sure if I can give a satisfactory explanation why 2+2=4. (Ep. 6)
    • Abstract algorithms replaced material and visual techniques for a reason. They are more efficient (Tom Bennett & Daniel Ansari).
    • Math manipulatives can hinder automaticity. Kids generally understand the concept but they can’t do the exercises (Matthew Burns). Sometimes they just need tons of practice.
  • Teaching problem-solving explicitly is a fool’s errand. Solving complex problems is an emergent phenomenon from mastery of the basics (Greg Ashman). Barbara Oakley‘s research shows that practice leads to creativity. Memorize the basics early so you can dance later (Lucy Crehan & Daisy Christodoulou).
  • We don’t need a balance between teaching basic facts and teaching complex problems. A pendulum is the wrong metaphor. A better metaphor is that knowledge is the path way to skill (Daisy Christodoulou).

Science of Learning

  • Learning styles don’t exist. Teaching according to learning styles doesn’t improve results ( Daniel Willingham).
  • Students benefit from taking notes but also benefit from having complete notes as they only write down about half of the relevant info
    • I use fill-in-the-blank notes to get the best of both worlds.
  • Remove extraneous elements of your teaching that overwhelm working memory for no reason. Keep it simple and scaffold up to eventually slowly remove the scaffolds. Remove distractions and highlight the important (Zach Groshell).
  • It’s important to block until near mastery and then interleave to deepen understanding (Patrice Bain).

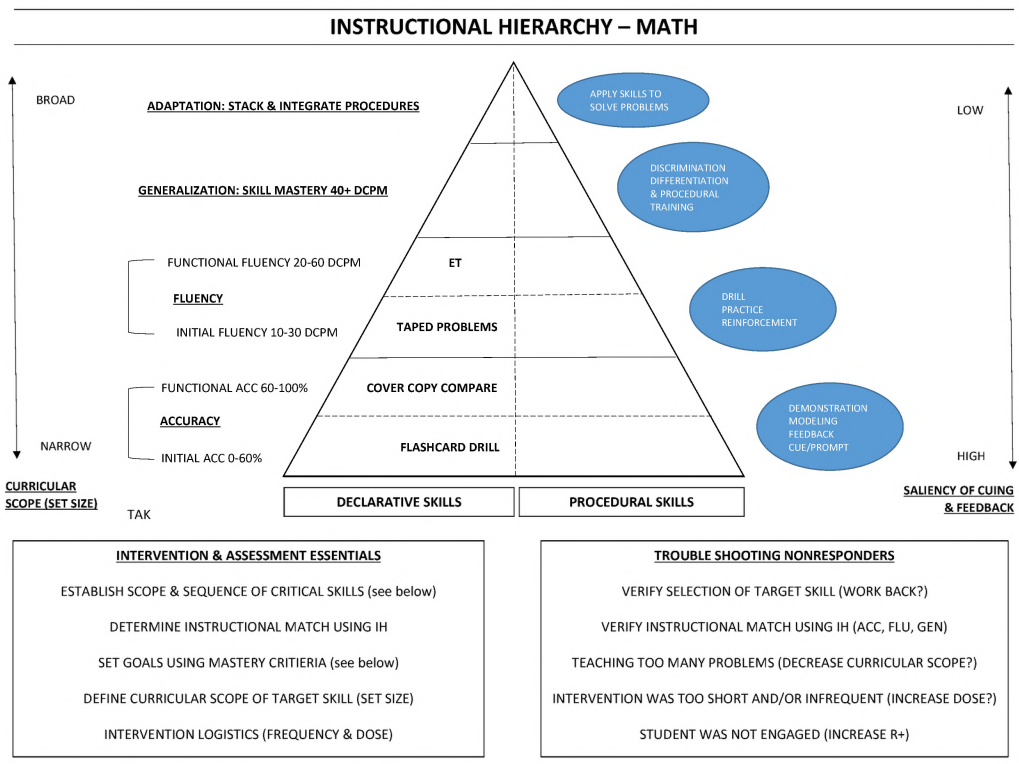
My definition is conceptual understanding is demonstrated when students have the necessary declarative facts needed to solve the problem, can accurately and explicitly state the procedures needed to complete the problem, can explain when, how, and why to implement each step required to solve the problem.

Brian Poncy – Episode 30
  • Learning Hierarchy (Matthew Burns & Brian Poncy):
    • Modelling with corrective feedback until sufficient accuracy.
    • Increasing speed and accuracy (fluency)
    • Eventually leads to generalization.

Evaluation

  • Cumulative testing makes use of spaced retrieval and interleaving, which aligns with the science of learning.
  • Having high expectations is a necessary, but not a sufficient condition for learning. Nearly everyone can reach mastery of K-12 concepts. (Tom Bennett & Daniel Willingham). We expect everyone in our society to have the ability to read. We should have the same expectations for basic numeracy (Daniel Ansari).
  • Rate-based metrics are more reliable indicators of students’ instructional levels than accuracy alone. Timed tests are necessary to assess students’ fluency skills (Robin Codding).
  • Standardized scores are better than arbitrary letter grade categories (Daisy Christodoulou).
    • Student attainment is a smooth continuum like age. It doesn’t make sense to draw lines in the sand and create groups such as young, adult, and old.
    • Standardized scores also differentiate between easy and hard tests whereas percentages do not. It might be better to score 20% on a difficult test than it is to score 60% on an easy test (see this video to learn more about standardized scores).
  • Standardized tests may be less biased than no test and only teacher judgement and global evaluation (Daisy Christodoulou).

Homework

  • The homework should not introduce any new concepts. Eliminating homework altogether disproportionately hurts students who struggle.
  • Only provide final answers to homework problems. Work through hard homework problems in class the next day or as per student request 1-on-1 (Ep. 16).
  • Marking homework for feedback is not super effective. Spare yourself the trouble (Tom Bennett).

Emotions

  • Stress can be helpful during the encoding phase, but is not during the retrieval phase (Dan Rosen). Tons of low-stakes or no-stakes practice is a great way to reduce stress by increasing learning with spaced retrieval and interleaving (Dan Rosen).
    • The relationship between math anxiety and timed tests is complicated and not necessarily harmful. We shouldn’t get rid of exams (Dan Rosen).
    • The relationship between math achievement and math anxiety is bidirectional, with higher math anxiety associated with lower math achievement and vice versa. Early poor math performance may have a stronger impact on later math anxiety (Robin Codding).

We need something like the FDA for educational practices.

Matthew Burns

Education Policies

  • Quality textbooks have their place in k-12 (Ep 8). What’s fundamentally better about worksheets? Especially created by teachers tight on time and with limited resources.
  • Teachers need better training. Teacher’s college is a farce and far from being evidence-informed. Internships are where most of the learning occurs, unfortunately.
  • The train analogy: A curriculum with fewer concepts and more depth is probably best (Lucy Crehan).
  • The shadow education system: Many of the highest math achievement country have after-school tutors as part of the culture (Ep 8).
  • The two definitions of equity:
    • To what extent does the students’ background correlate or predict their achievement?
    • Those who do the worst, how badly did they do? What proportion of students managed to get at least baseline levels?
  • Should we stop teaching math because of the differences in outcomes? No (Brian Conrad).
    • A quality public education system is key for equity. Wealthy families will find a way to self-insure and get access to quality education somewhere else.
  • Traditional knowledge such as the alphabet and the numbering system have stood the test of time. Revamping curriculums to teach 21st cutting-edge skills at the expense of literacy and numeracy is dangerous (Daisy Christodoulou).
  • There are no consistent large gender differences in math outcomes. However, girls tend to do better at reading tasks than boys (Daniel Ansari). We should avoid designing instruction based on gender.

Class Management

  • Working in groups on the whiteboards is probably overrated. Social loafing, plagiarism and distractions are some of the factors that get in the way of learning. The amount of buzz in the classroom is no measure of engagement. The only measure of engagement is the amount of thinking and updating in student’s heads (which makes no sound).
    • Rows and columns is still probably the best class layout (Tom Bennett).
  • Mobile phones have no place in schools and stricter policies should be enforced (Tom Bennett & Daniel Willingham).

All Snips

Affiliate Links

Recent Articles