Peter Attia wrote a series of blog posts that get into the nuances of science and research. This article is a summary of the notes I took while reading Peter’s material. I added some things I picked up from my master’s degree in statistics. Most statistics degrees do not get practical. Seldom are the statistical assumptions perfectly met in practice. Consider this as an exposé of how statistics and research can go wrong but also of why we need them to check our assumptions.
Main Takeaways
- Don’t just read the headlines. Always ask about relative risk versus absolute risk.
- Epidemiological findings do not tell us if we are at an increased or decreased risk of some disease. They only say that this particular environmental factor is associated with risk.
- Correlation does not imply causation. Doing more and more observational studies might not move us towards the truth. The vast majority of observational claims are not replicated by randomized-controlled experiments.
- Randomization-controlled experiments are the best tool we have. We still make big mistakes with this tool. It is incredibly difficult to pick up the signal instead of the noise. We might not be able to pinpoint the truth, but we can hope to limit the ways we might be wrong.
- Our society is willing to commit more type II errors than type I errors. We are willing to say that a drug does not work about 20% of the time when it really does. However, we are only willing to say that a drug works when it does not about 5% of the time.
Read the original articles
- Studying Studies: Part I – relative risk vs. absolute risk
- Studying Studies: Part II – observational epidemiology
- Studying Studies: Part III – the motivation for observational studies
- Studying Studies: Part IV – randomization and confounding
- Studying Studies: Part V – power and significance
Part I – Relative Risk vs. Absolute Risk
The first principle is that you must not fool yourself—and you are the easiest person to fool.
Richard Feynman
- Bend over backwards to show how you’re maybe wrong.
- The two statements below are equivalent.
- New drug reduced cancer incidence by 50%. (Relative Risk)
- New drug reduced cancer incidence from 2 per 1000 to 1 per 1000. (Absolute Risk)
- Always report both the absolute risk (AR) and the relative risk (RR) to provide context. They are two sides of the same coin. You can only see the the entire coin once you know both the absolute risk and the relative risk.
- Absolute risk is more useful at communicating the true impact of an intervention.
- Relative risk is more flashy for the news. Most people misinterpret RR.
| Treatment Group (T) | Control Group (C) | Total | |
| Events | 15 | 100 | 115 |
| Non-Events | 13,500 | 13,400 | 26,900 |
| Total Subjects | 13,515 | 13,500 | 27,015 |
![]()
![]()
![]()
It’s hard to get out of bed to read about a whopping 0.63% reduction in absolute risk when you could be reading about a—wait for it—85% relative risk reduction!
Peter Attia
Part II – Observational Epidemiology
All human knowledge is limited to working back from observed effects to their cause.
Claude Bernard
- We see something happen in the world and automatically assume their has to be a cause for it. We tend to think that the thing that occurred immediately before the new thing must have caused it. It is certainly true for many vents at the macro level.
- Hippocrates is the first known epidemiologist. He looked at how environmental factors affected disease.
- Epidemiological findings don’t actually tell us if we’re at increased or decreased risk of a disease.
- They only tell us that the environmental factor is associated with risk.
- These associations can be useful to generate ideas for experiments.
- It might also help us guess at the effect size of a specific treatment.
- Theory determines measurement.
- You can test your assumption that there is an association between two things with an observational study (Hypothesis-testing).
- You simply cannot infer causation even if there is a strong association.
- Funny examples of bizarre correlations.
- Randomized experiments are more expensive than observational studies but may give a better return on investment (ROI) in terms of reliable knowledge output.
Typically, doing more and more observational studies doesn’t get us any closer to the truth.
Peter Attia
For me, I am driven by two main philosophies, know more today about the world than I knew yesterday. And along the way, lessen the suffering of others. You’d be surprised how far that gets you.
Neil deGrasse Tyson
Part III – The Motivation for Observational Studies
Why are randomized-controlled trials rare?
- RCTs are expensive
- RCTs are long
- Quality RCTs are hard to do
- falsifiable hypotheses
- clear objectives
- proper selection of endpoints
- appropriate subject selection criteria (both inclusionary and exclusionary)
- clinically relevant and feasible intervention regimens
- adequate randomization, stratification, and blinding
- sufficient sample size and power
- common practical problems
RCTs try to establish cause-and-effect relationships that help the individual whereas epidemiologists try to establish associations that harm the population.
Peter Attia
- Most observational claims are not validated were tested in subsequent randomized trials.
- Sometimes randomized-controlled trials suggest the oppisite of an observational claim.
Common types of biases?
- Healthy-user bias
- Vegetarian are more likely to be health-conscious than the average meat-eater.
- Cigarettes and lung cancer likely had fewer confounding factors in the past where a larger proportion of people smoked. Smokers today are more likely to be less health-conscious.
- We can predict that the observed hazard ratios will increase with less and less people smoking.
- “Epidemiologic survey of smokers today will have a harder time identifying cause and effect.” – Peter Attia
- Confounding bias
- A third variable might explain a strong relationship between two variables.
- A classic example.
- Information bias
- Low accuracy of measurement.
- Availabilty & Recency biases are common with food questionaires.
- Reverse-causality bias
- Diet soda => Obesity or Obesity => Diet soda
- Selection bias
- Your sample is not representative of the population.
- The Nurses’ Health Study does not represent the population.
Common types of studies?
- Retospective cohort studies
- Look in the past and conduct an analysis based on data that already happened.
- Prospective cohort studies
- Design an experiment. The word experiment makes it sound legit.
- NOTE: There is still no randomization which eliminates the possibility of causal inference.
Part IV – Randomization & Confounding
There is no cost to getting things wrong. The cost is not getting them published.
Brian nosek
- The two main techniques to “controll” or “adjust for” confounders
- Include variables as regressors.
- Becomes multivariate regression.
- Is the best technique when you have many confounders.
- Stratify the data on these confounders.
- Randomized-block desgin.
- Works best when the number of confounders is small.
- You want your blocks/strata to be homogeneous within each block but heterogeneous between blocks.
- Include variables as regressors.
- “Effect sizes of the magnitude frequently reported in observational epidemiologic studies can be generated by residual and/or unmeasured confounding alone.”
- Could the observed phenomenom be caused by some unmeasured variable?
- The problem of trying to control for multiple confounders.
- The typical interpretation of the slopes of a multivariate linear regression model is something like this:
- If we increase
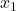 by 1 unit and hold all the other
by 1 unit and hold all the other 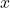 ‘s constant, then
‘s constant, then 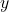 increases by
increases by 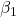 .
.
- If we increase
- In practice, you often can’t hold all other variables constant because they are correlated (multicollinearity).
- Ideally, we want our predictor variables (
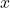 ) to be independent of each other.
) to be independent of each other.- Changing
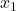 does not change
does not change  .
.
- Changing
- Ideally, we want our predictor variables (
- The typical interpretation of the slopes of a multivariate linear regression model is something like this:
- Most non-randomized studies still extrapolate to suggest real-world applications.
- RCTs are need to infer causal relationships.
- Recall that many/most observational claims are not validated by controlled experiments.
- Many of these reccomendations based on “the research” could violate the “Do no harm” principle.
- The individual researcher rarely thinks they do bad science.
- More than 90% of people in the US put their own driving skills in the top 50%.
- A research claim could be more likely to be false than it is to be true.
- Does lack of correlation imply lack of causation?
- Observational studies may be more useful to show the absence of causal relationships than the presence of causal relationships.
- We can never be certain.
Some Common Models
- Linear Regression
- We try to fit a line through the data points.
- Our brains like to think that our universe was designed using a ruler.
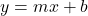 when we have only two variables (no confounders)
when we have only two variables (no confounders)- NOTE: In statistics you’ll often see
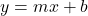 written as:
written as:  where
where  is the error term (residuals) because our equation does not the data perfectly
is the error term (residuals) because our equation does not the data perfectly
- Logistic Regression
- Can deal with binary depedent variables.
- Extrapolation using regression is not always applicable.
- Interpolation is safer, but it is still an assumption.
- Can deal with binary depedent variables.
Part V – Power & Significance
- The vast mojority of published literature reports statistically significant results.
- Always assume no relationship (null-hypothesis
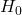 )
)- This is similar to our justice system.
- People are assumed to be innocent until proven guilty beyond a reasonable doubt
- beyond a reasonable doubt = statistically significant
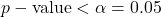 where
where- the
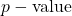 is the probability that reject a true null hypothesis?
is the probability that reject a true null hypothesis? - What is the probability that to commit someone as guilty when they are in fact innocent?
- What is the probability that the effect (i.e., the difference between the groups) you are seeing is not due to the effect of the treatment versus that of placebo, but instead is due to noise, or chance?
- This is similar to our justice system.
 is the significance level (typically set at or below 5%).
is the significance level (typically set at or below 5%). 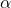 is the probability of a false positive.
is the probability of a false positive.- In practice 5% has proven to be good enough.
- We are metaphorically willing to put inoccent people in jail 5% of the time.
- Statistical significance vs. Practical significance.
- Sometimes a result is not statiscally significant but can be practically significant.
- The sample size was not big enough, but the difference between groups (effect size) was relatively large.
- Maybe the researcher chose a significance level of 0.001 instead of the typical 0.05.
- A large sample size can lead to significant p-values although the effect size is not practically significant.
- You could detect such small differences with a large enough
 even if the two groups were given a placebo.
even if the two groups were given a placebo.
- You could detect such small differences with a large enough
- Results were NOT statistically significant:
- What magnitude of difference (i.e., effect) was the study powered to detect?
- Is it possible the effect was present, but not at the power threshold?
- Results were statistically significant:
- How big is the effect (i.e., the magnitude of difference between groups)?
- How many people did you look at to detect the effect?
- Sometimes a result is not statiscally significant but can be practically significant.
- Common misusages of statistics:
- data dredging, p-hacking, fishing expeditions, researcher degrees of freedom, gardens of forking paths
- Use the Bonferroni Correction to remmediate this problem.
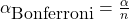
 is the number of tests you conduct on the data.
is the number of tests you conduct on the data.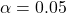 means that we have a 5% chance that the results were due to chance instead of a “real” difference. If you roll a twenty-sided die twenty times, you can expect the number 7 to appear once on average.
means that we have a 5% chance that the results were due to chance instead of a “real” difference. If you roll a twenty-sided die twenty times, you can expect the number 7 to appear once on average.
- The two ways to go wrong in a trial:
- You put an innocent person in jail (false positive).
- You reject the null-hypothesis (
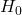 ) although it was true.
) although it was true. - We really try to avoid this type of error. We don’t want to tell someone they have cancer when they don’t.

- You reject the null-hypothesis (
- You declare a guilty person to be innocent (false negative_.
- You fail to reject the null-hypothesis although it was false.
- In practice, the cost of having criminals on the street is less than commiting innocent folks to jail. We prefer to let a cancer go untreated than to treat a cancer that is not there.
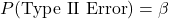
- You put an innocent person in jail (false positive).
Statistical Power
![]()
- What affects statistical power?
- The probability of a false positive (Type I error) result (α)
- The sample size (N)
- The effect size (the magnitude of difference between groups)
- The false negative (Type II) error rate (β)
- Effect size is determined after the experiment.
- Review litterature to estimate effect size prior to experiment.
- Run a pilot study to estimate effect size.
- The typical standard for the power of a study is 0.8.
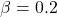
- There is a 1-in-5 chance of a false negative.
- Note that we are willing to tolerate
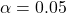 but
but  can be 0.2.
can be 0.2.
- How can you dtermine the sample size to have a high enough power?
- http://powerandsamplesize.com/Calculators/
You can check out Peter Attia’s Nutritional Framework if you’ve enjoyed this article.
