How To Think About Teaching

Reading Time: 10 minutes
Post Views: 76

Background

I teach high school math and physics in Ottawa, Canada. I realized fairly quickly that teachers don’t get adequate training before entering the classroom. In teacher’s college, I was taught things that do not align with the research. Now that I teach, the rare training we get often lacks evidential support and lacks consistency from session to session. Teachers leave conferences with a bunch of tricks that don’t necessarily fit together and have no way of judging which one to prioritize. We shouldn’t need to learn what matters outside of school hours. Teachers are left forced to blindly adopt the latest and shiniest educational fad that promises to fix the educational system.

This started to change when I discovered Anna Stokke’s Chalk & Talk podcast. Since then, I’ve read many books and research papers, tested ideas in my classrooms, and attended the Toronto ResearchEd conference. I’m writing this article to provide a synthesis of what I’ve learned from this intellectual rabbit hole and my years of experience as a teacher and tutor. This piece will be divided into two separate articles. In this article, I’ll try to clarify my teaching objective and provide a general strategy for how to teach based on research. In the next, we’ll get practical and discuss how I implement many of the principles in my classrooms (tactics).

Objective

The objective of teaching is to bring as many students as possible to a mastery level (>= 85%) on the curriculum‘s overall and specific expectations.

Mastery learning was first proposed by Benjamin Bloom in 1968. He postulated that:

Most students, perhaps over 90 percent, can master what teachers have to teach them, and it is the task of instruction to find the means which will enable students to master the subject under consideration. A basic task is to determine what is meant by mastery of the subject and to search for methods and materials which will enable the largest proportion of students to attain such mastery.

It has been my experience and the experience of others that the vast majority of students can excel and truly master the Ontario curriculum. The curriculum was designed with this in mind as it doesn’t teach differential equations to four-year-olds.

Defining mastery is not trivial. Here’s how Khan Academy draws the lines in the sand.

A classroom teacher might draw the line at 85% or A-. This margin of error allows for mistakes of misreading a question or making little mistakes of calculation. It’s rare for teachers to get 100% on their own assessments.

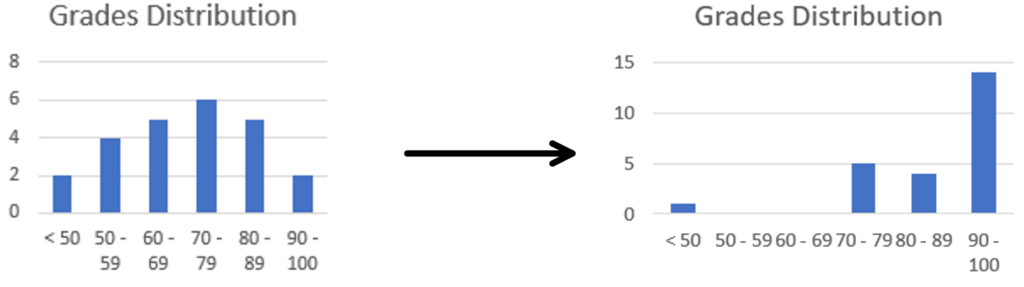
It’s important to recognize that mastery lies on a spectrum. A student doesn’t magically go from knowing nothing at 77% to knowing everything at 86%. More precisely, the function of teachers is to shift the normal distribution to the upper end of the performance range. Here’s what Bloom had to say on the topic:

There is nothing sacred about the normal curve. It is the distribution most appropriate to chance and random activity. Education is a purposeful activity and we seek to have the students learn what we have to teach. If we are effective in our instruction, the distribution of achievement should be very different from the normal curve. In fact, we may even insist that our educational efforts have been unsuccessful to the extent to which our distribution of achievement approximates the normal distribution.

Criticisms of the Objective

The obvious critique of this objective is that academic achievement is not the only thing that matters. We ultimately want our students to be good citizens with socio-emotional skills and good learning skills and work habits. Not many people would argue that these are not worthy goals. That said, grades are the measurable byproduct of the other variables. Grades are a catch-all statistic. Academic achievement is a proxy for who we want our students to be when they exit the education system. It’s far from perfect (see Goodhart’s law), but it’s the best we got. Learning how to learn is more important than learning any specific concept. However, how do we measure the ability to learn if it’s not through traditional assessments?

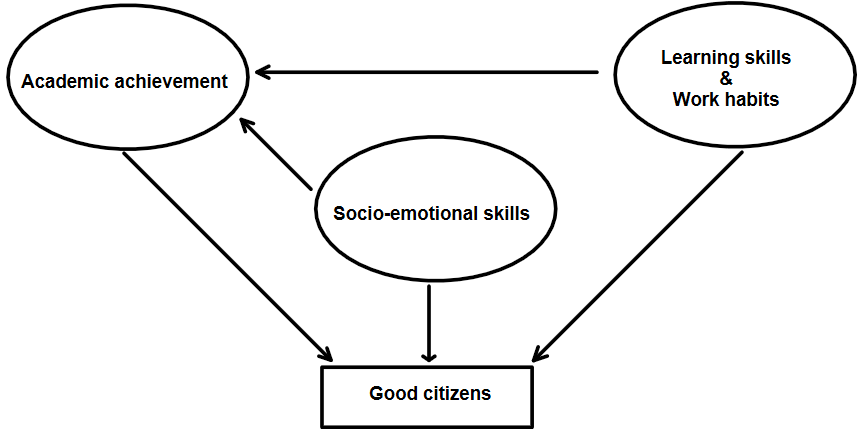
Furthermore, I’ve yet to meet parents who don’t value high grades. Not only do they value the entry ticket to post-secondary education, but they also value learning for its own sake. Many of the expectations of Ontario math curriculum do align with the goal of creating good citizens. Let’s consider a few from the new grade 9 math course (MTH1W) :

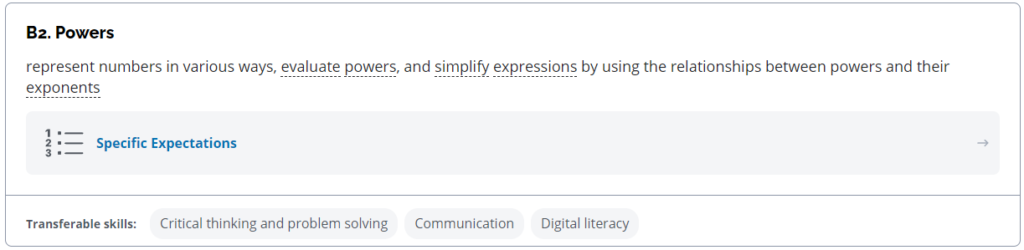
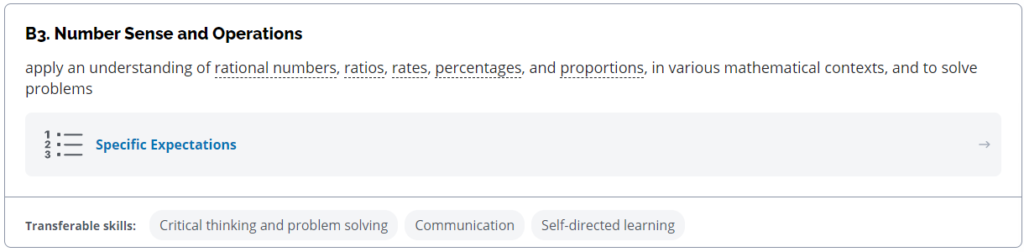
It’s difficult to argue that mastering these concepts wouldn’t be a worthwhile endeavour. Most are directly applicable to daily life or the job market. Other expectations such as applying exponent rules (B2) may not be useful in day-to-day life, but they are a fundamental stepping stone to progress in mathematics, and thus, many STEM careers. Many concepts learned in high school are mostly useless unless continuing in STEM. Given the hierarchical nature of mathematics, students have to learn abstract concepts to build their edifice of knowledge.

Now that we have the clear goal of maximizing the number of students who reach mastery, we can transition and start thinking about the strategy we’ll use to get there.

Strategy

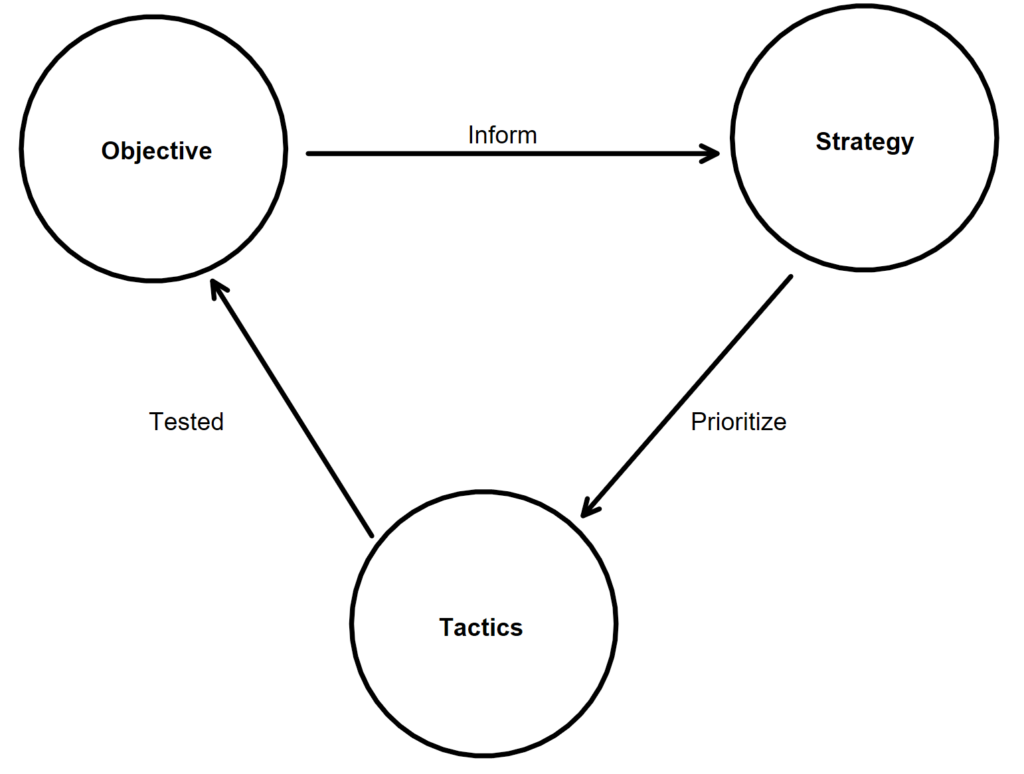
To achieve our objectives, we first need to have a strategy: an overall approach, a conceptual scaffolding or mental model that is informed by science, is tailored to our goals, and gives us options. Our specific tactics flow from our strategy, and the strategy derives from our objective.

Peter Attia – Outlive

Tactics are the specific things you do in a classroom such as grading homework, greeting students at the door, flipping the classroom, etc. Teachers are bombarded with tips, tricks, and ideologies of how they should run their classrooms. Recommendations from colleagues, the principal, the school board, teacher training, books and blogs, or research often contradict each other. How is a teacher supposed to select and reflect on specific pedagogical practices?

Without an understanding of the strategy, and the science that informs it, our tactics will not mean much, and you’ll forever ride the merry-go-round of fad diets and trendy workouts and miracle supplements.

Peter Attia – Outlive

Substitute “fad diets and trendy workouts and miracle supplements” in the quote above with the latest and shiniest teaching ideology that promises to revolutionize or “fix” the education system. Having a clear strategy informed by our objective and science is the antidote to educational “fad diets”.

A good strategy allows us to adopt new tactics and discard old ones in service of our objectives.

Peter Attia – Outlive

A strategy is the lattice of knowledge and prism through which we evaluate tactics. Our strategy needs to be informed by evidence and revised over time as we learn more about how to teach. The challenge is that, like in nutrition, educational research is messy and not all sources of evidence should be weighted equally. I recommend this podcast episode on the red flags in education research with Ben Solomon (Ep 23) to learn more about educational research limitations.

Below is a rough hierarchy of the reliability of evidence sources:

  1. Randomized Controlled Trials (RCTs and experimental research are rare in education)
  2. Meta-analyses (See John Hattie’s work and its criticisms 1 & 2)
  3. Research in adjacent fields such as cognitive science, neuroscience, psychology, anthropology, etc.
  4. Formal or informal research and experiments performed at your school or in your classrooms.
  5. Personal experience and veteran teacher field wisdom.

Notice that anecdotes and personal philosophies are at the bottom of the list. Yet most of the advice we receive is based on this data source. It’s useful to distinguish between our strategy needing to be “evidence-informed” and not “evidence-based or evidence-bound”. There are very few specific recommendations from research that will work for all students in all contexts. As Daniel T. Willingham said at ResearchEd: “If teaching would be strictly restricted to evidence-based practices, then your teaching day would end at 9:15 AM.” We don’t know that much with absolute certainty. This further supports the need for a comprehensive strategy. Domains such as making a peanut butter sandwich don’t require a strategy. The proper tactics will suffice. It’s the domains in which we cannot immediately evaluate the efficacy of our tactics that need a working strategy.

It’s not because research is messy that we should abandon trying to figure out what works. We shouldn’t throw out the baby with the bath water. Below are some of the evidence-informed principles that stood the test of time. Together they form the hubs of my web of mental models and are the pillars of my strategy.

Assessment

What gets measured gets managed. What gets managed gets done.

Our objective is to ensure as many kids master the curriculum expectations. Hence, we must validly and reliably measure student mastery. Otherwise, there’s no feedback mechanism for our pedagogical practices and the student’s learning process. In the tactics article, we’ll dive deeper into specific practices for useful assessment. I recommend watching Ken O’Connor’s lectures (I & II) to challenge how we traditionally approach assessments.

Equity & Differentiated Instruction

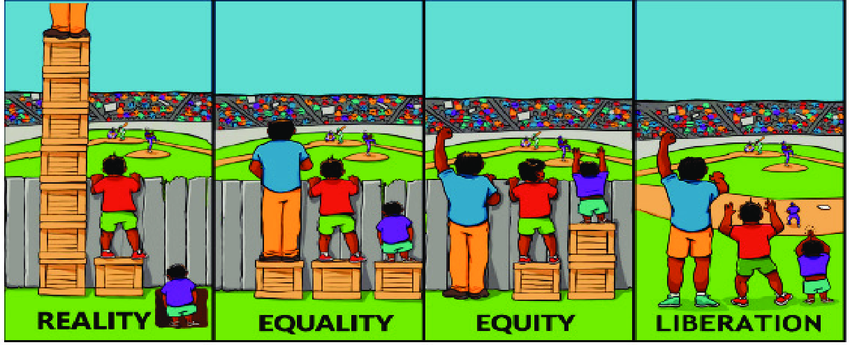
Many of us have seen the picture above. While removing barriers is ideal, it’s often impractical and resources are best spent on equity practices. The OECD differentiates between two types of equity:

Equity as inclusion means ensuring that all students reach at least a basic minimum level of skills.
Equity as fairness implies that personal or socio-economic circumstances, such as gender, ethnic origin or family background are not obstacles to educational success.

OECD – Equity and Quality in Education

Our objective of maximizing the number of students who reach a mastery level of the curriculum‘s standards aligns directly with the first definition of equity as inclusion. There is a subtle difference, however. Our goal is to bring everyone to mastery. The equity definitions above would both be satisfied if everyone scored “a basic minimum level of skills” (say a level 2 in Ontario) regardless of their socio-economic circumstances. Our objective is bolder which increases the need for effective tactics.

Although most agree with the objective, fewer accept its implications. Few teachers brag or feel good about giving no “boxes” to the students on the left in the picture above. Our instinct for equality is deeply rooted (see capuchin monkeys given grapes and cucumbers). Yet, our objective implies that teachers should allocate most of their time to the students who have not yet reached mastery.

The exact allocation of resources is up for debate. Should teachers first help students who are close to mastery but need a little nudge? Should the teacher instead start by helping the students furthest from mastery? Should teachers allocate their time based on their estimated return on investment? If so, should a teacher ignore students who stubbornly refuse to be on task and instead focus on the students who are “ready to learn”? What we think about these questions will affect our tactics (see AR glasses).

The Science of Teaching and Learning

Psychology, neuroscience, and cognitive science can inform how we design instruction. One key finding is that learning styles are mostly debunked (see Daniel T. Willingham). Human brains learn in similar ways. Cognitive load theory claims that we learn best by breaking tasks into small parts and automating basic facts and skills to avoid overwhelming working memory (see this article). I suggest watching Dan Wolczuk’s primer on Cognitive Load Theory and Nidhi Sachdeva’s videos on How Learning Happens.

Many researchers define learning as “a change in long-term memory.” Our role as a teacher is to use effective teaching methods to maximize long-term memory changes. Another key finding is that practice is necessary for learning to happen. Retrieval practice is an effective way to slow the forgetting curve and increase fluency. Again, we’ll discuss specific implementations of these principles in the next article.

Amanda Vanderheyden and Matthew Burns propose the following instructional hierarchy. This framework informs how we’re going to introduce new concepts to students. If they are in the “acquisition” phase, then we’ll incorporate more modelling with corrective feedback until they reach sufficient accuracy, say 85%).

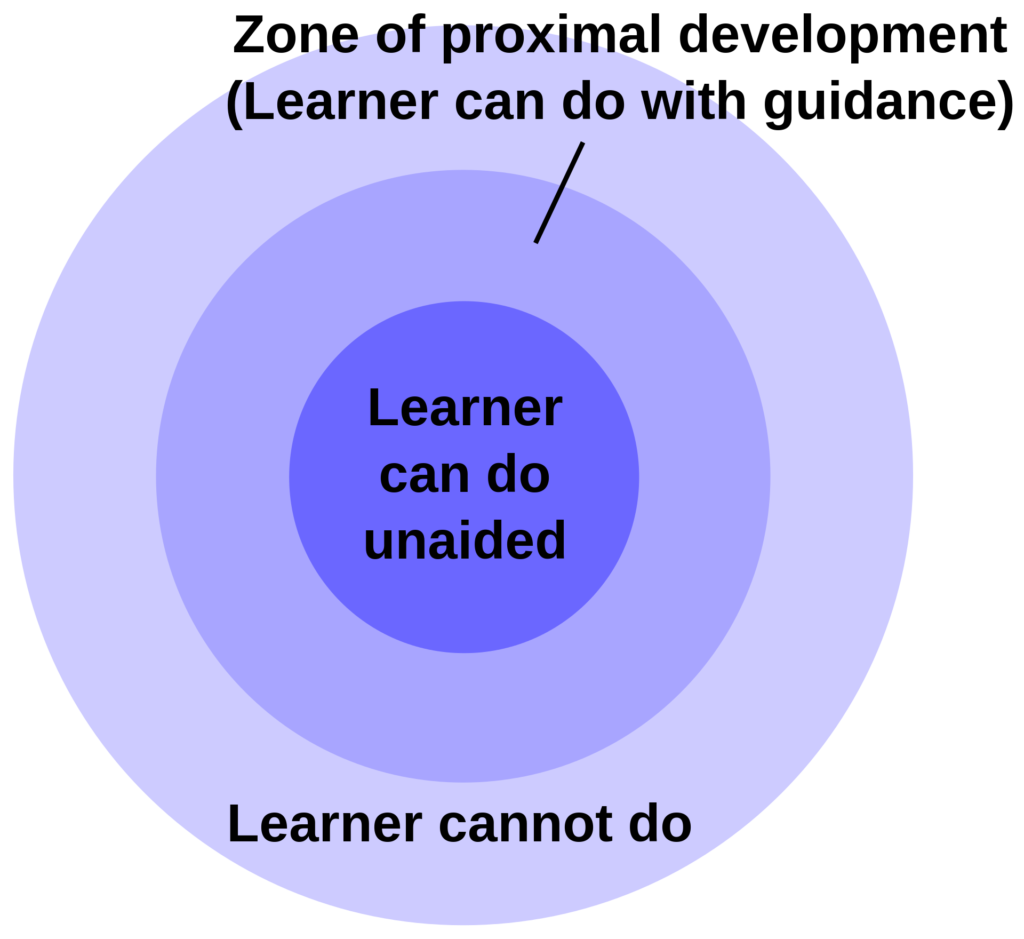
Lastly, a theoretical framework that I always return to is called the zone of proximal development. It was first introduced by Lev Vygotsky but has been developed by many other researchers such as Mihály CsíkszentmihályiLastly, a theoretical framework that I always return to is called the zone of proximal development (ZPD). Athletes and peak performers often call it the zone. The idea was first introduced by Lev Vygotsky but has been augemented by many others such as Mihály Csíkszentmihályi with his research on flow and Daniel Pink’s work on motivation.

It refers to the idea that learning is maximized when the learner stretches their limits but not too much. The role of the teacher is to keep their students in the zone by using scaffolds if the task is too complex or by increasing the difficulty of the problems if it’s too easy. John Mighton suggests that learning is optimized when the accuracy rate of students is around 85%. Making a few mistakes means the student is stretched beyond their current ability zone. However, making too many mistakes demotivates students and is an opportunity for teachers to scaffold until the rate of mistakes is relatively low. If learning happens, the nature of the mistakes will change.

Parting Thoughts

Strategy without tactics is the slowest route to victory. Tactics without strategy is the noise before defeat.

Sun Tzu

Theory alone is useless. Tactics alone are no guarantee of moving towards our objective. This article laid the foundation for how we can evaluate our pedagogical choices and filter the signal from the noise. The next article contains a non-exhaustive list of time-tested and evidence-informed practices for teachers.

Read This Next

Recent Articles