We all have been asked to buy raffle tickets to support a good cause at some point in our lives. I was recently asked if I wanted to buy tickets for my friend’s Buck and Doe celebration. It is a Canadian tradition meant to raise money for a couple’s wedding or honeymoon.
There are two ways to tackle the question of whether or not I should buy tickets.
- The human way. It is a fundraiser. I would not hesitate to pay for my friend’s meal or anything $20 or less so why would buying a $20 ticket differ?
- The math nerd way. Maybe I could calculate the expected value of buying a ticket and try to maximize my returns.
As you probably guessed, I opted for the second one. Technically, I acted like any other human being and bought a ticket without hesitating. The math journey came after the purchase of the ticket.
Estimating the value of each prize
| Prize | Description | Estimated Value ($) |
| 1 | 65″ 4K Smart TV | 1200 |
| 2 | YETI – Roadie 24 Hard Cooler | 200 |
| 3 | $100 Cash Prize | 100 |
I assumed the retail price of the average TV and cooler. Of course, this a rough estimation. You most likely could not sell these items for their original prices. However, these items have some inherent value. The organizers of such raffle lotteries often buy these new items at discounted prices or receive prize donations to increase their profit margins.
How many tickets do they need to sell to break even?
The total estimated value of prizes they are giving away is $1500 ($1200 + $200 + $100). Each ticket costs $20. Thus, they need to sell at least 75 tickets to break even (
). Feel free to explore the relationship between profit and tickets sold with the animation below. For example, the organizers may want to raise $5000 for their wedding. Once they have the profit equation, they simply need to solve for the number of tickets sold. For this example, they would need to sell at least 325 tickets to raise $5000. You can click on the “edit graph on desmos” in the bottom right corner of the graph to change some values.
![\[P(t) = 20t -1500\]](https://duddhawork.com/wp-content/ql-cache/quicklatex.com-024db4059011ec557bdb75a43e15a5e4_l3.png "Rendered by QuickLaTeX.com")
![\[5000 = 20t - 1500\]](https://duddhawork.com/wp-content/ql-cache/quicklatex.com-dfe0cd306e99c82740bd67db065efe4f_l3.png "Rendered by QuickLaTeX.com")
![\[t = \frac{6500}{20} = 325\]](https://duddhawork.com/wp-content/ql-cache/quicklatex.com-c49d7a59190126df12164b7d5847a111_l3.png "Rendered by QuickLaTeX.com")
What is my probability of winning a prize?
It depends on how many tickets you purchased and how many tickets were sold in total. If you only bought one ticket, then you cannot win all three prizes assuming they do not put the ticket back in the hat (without replacement). The probabilities might also depend on the order of the prizes drawn. We will assume that they pick the third prize, then the second, and pick the first prize last to build suspense.
Tree diagrams are a great way to calculate probabilities for relatively simple problems such as this one. Below is a tree diagram for one purchased ticket and 100 sold tickets. Note that you can win at most one prize if you only bought one ticket.
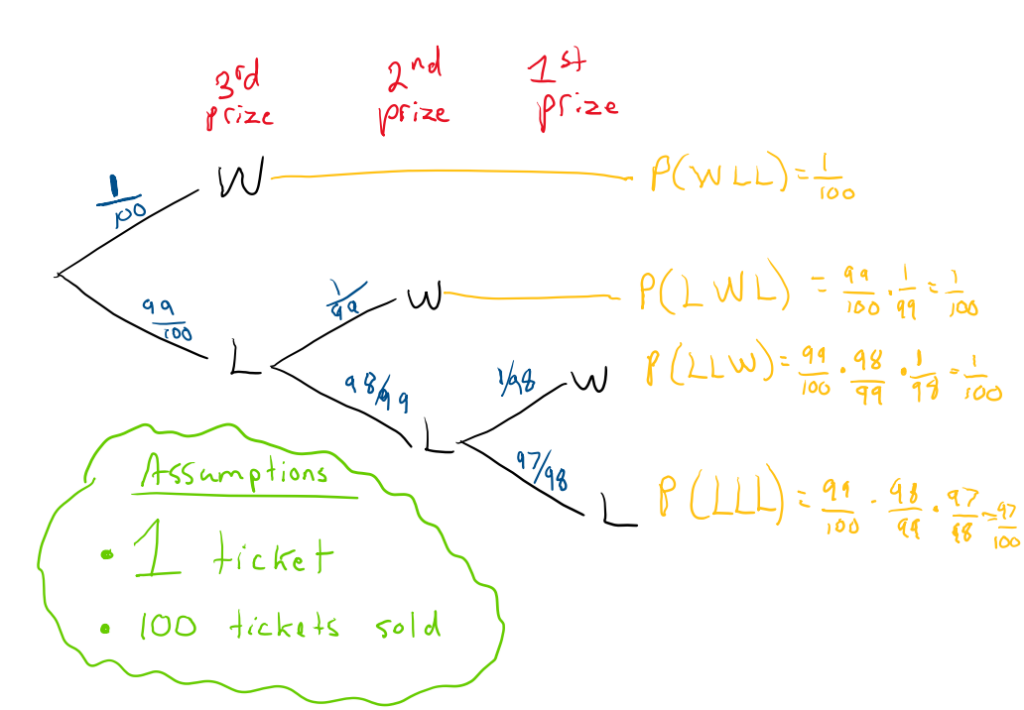
It is interesting to note that it is equally likely to win each prize in the example above. You have a 3% chance of winning something and a 97% of going home empty-handed. We can also compute the expected value (EV) of the previous example.
We can first calculate the expected value of buying no tickets.
![\[EV(n =0 , N) = P(\mbox{W}) \times (\mbox{Winnings}) - P(\mbox{L}) \times (\mbox{Losings}) = 0 \times (\mbox{Winnings}) - 1 \times 0 = 0\]](https://duddhawork.com/wp-content/ql-cache/quicklatex.com-aef2500805af15152e99ea0a8450bd49_l3.png "Rendered by QuickLaTeX.com")
It is no surprise that we can expect to win $0 if we do not buy any tickets. At least our EV is not negative.
To get the expected value of the draw with one ticket, we multiply the profits by the probability of winning each prize. For the first prize, we have a profit of $1180 since you win a value of $1200 and it costs you $20 for the ticket. Multiplying the profit by the probability of winning the first prize with one ticket results in $11.8. We can repeat this process for all four outcomes and we get an expected value of -5 dollars when we add them together. The negative EV tells us that it is not a mathematically sound bet to buy one ticket with the given prizes and if you knew that they sold 100 tickets.
| Prize | Estimated Value ($) | Cost of Tickets Purchased ($) | Profit ($) | Probability | Expected Value ($) |
| 1 | 1200 | 20 | 1180 |  | 11.8 |
| 2 | 200 | 20 | 180 | | 1.8 |
| 3 | 100 | 20 | 80 | | 0.80 |
| None | 0 | 20 | -20 |  | -19.4 |
| TOTAL | 1500 | TOTAL | TOTAL | 1 | -5 |
Below is what your results could look like if you played this lottery 1000 times (1 ticket purchased & 100 tickets sold). In this simulation, you would have been up by $1320 after 339 draws. However, we know that we have an expected value of -$5. You decided to keep playing thinking you could make your money back. After losing $3500 and playing this lottery 1000 times, you decide to call it quits. Your average loss per lottery was $3.50. The law of large numbers says that if you kept playing, your average loss per lottery would approach – $5.
Feel free to run the simulation yourself with a different seed to get similar results. After enough trials, the average winnings per ticket should converge to -5$.
Does it make sense to buy more tickets to increase your expected value?
We know that buying a single ticket when 100 are sold is not a profitable strategy. We can build other tree diagrams for more tickets since you could theoretically win all three prizes if you bought three or more tickets.
From Figure 4 above, it is impossible to win all three prizes with two tickets out of 100. You still have a 94% chance of not winning any prizes. Your expected value is now around -$10 instead of -$5 when you only bought one ticket.
Figure 5 tells us that we have a 1 in 161700 chance of winning all three prizes. We still have a 91% of not winning any prizes. Our expected value with 3 tickets is now -$15. It seems as though buying more tickets leads to losing more money in the long run. We can expand our tree diagrams to calculate probabilities for any combinations of tickets bought (
) and tickets sold (
).
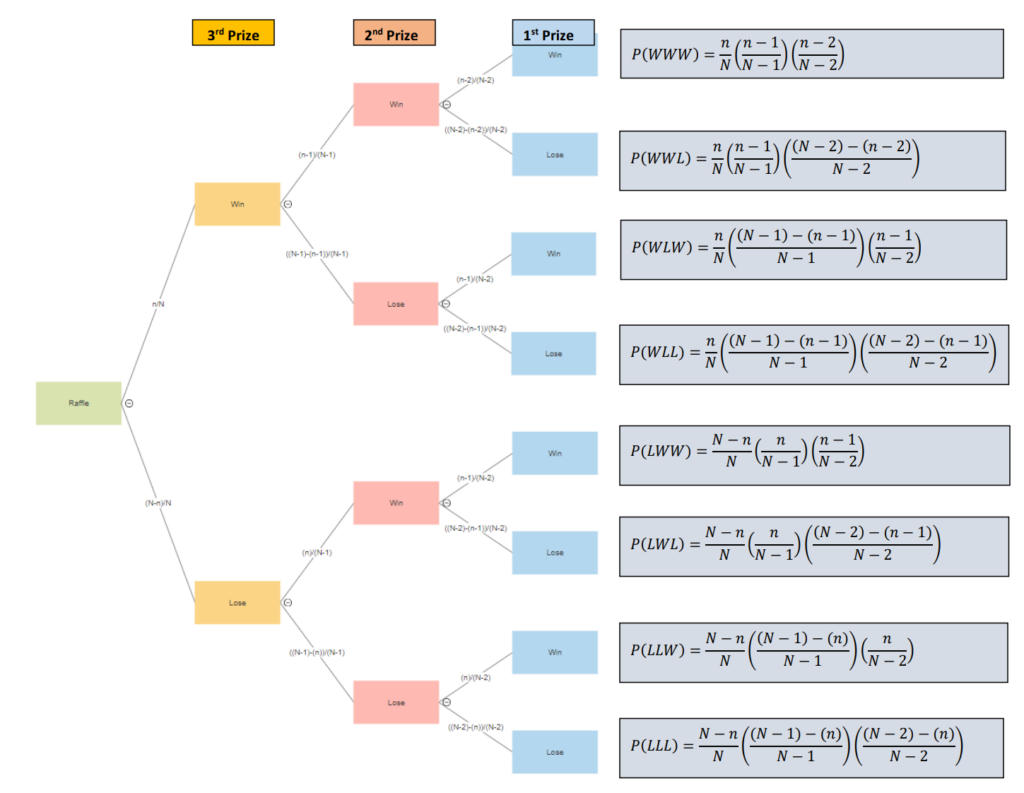
We can also visualize these probabilities in a Venn diagram to get a sense of the overlap between each event. You can refer to this article to get more practice with Venn diagrams.
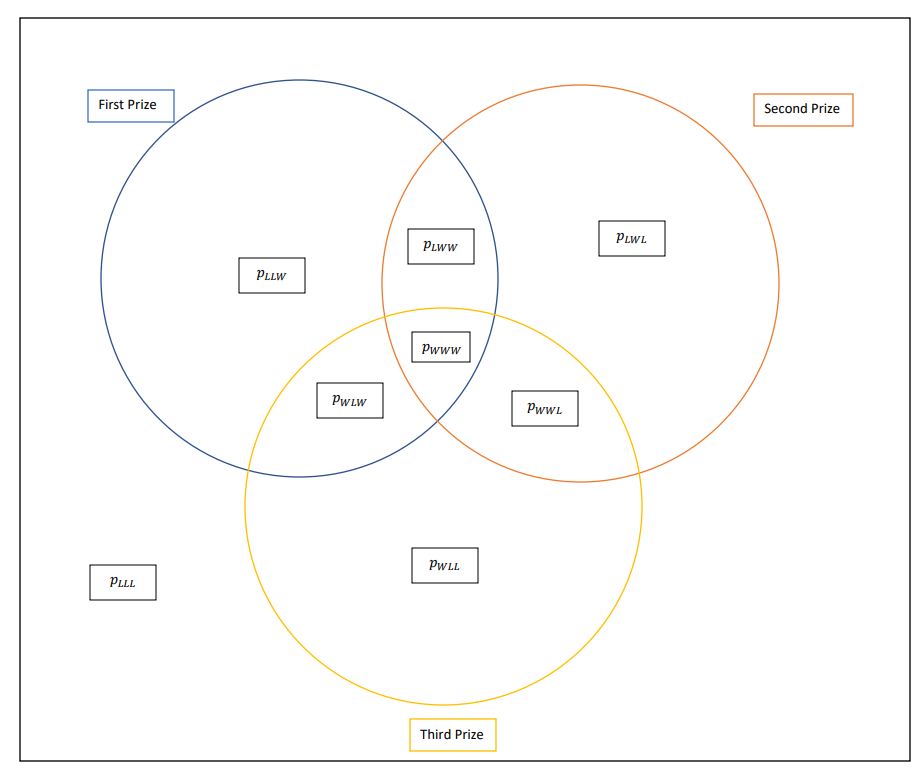
We can zoom in on the blue circle to get the probability of winning the first prize.
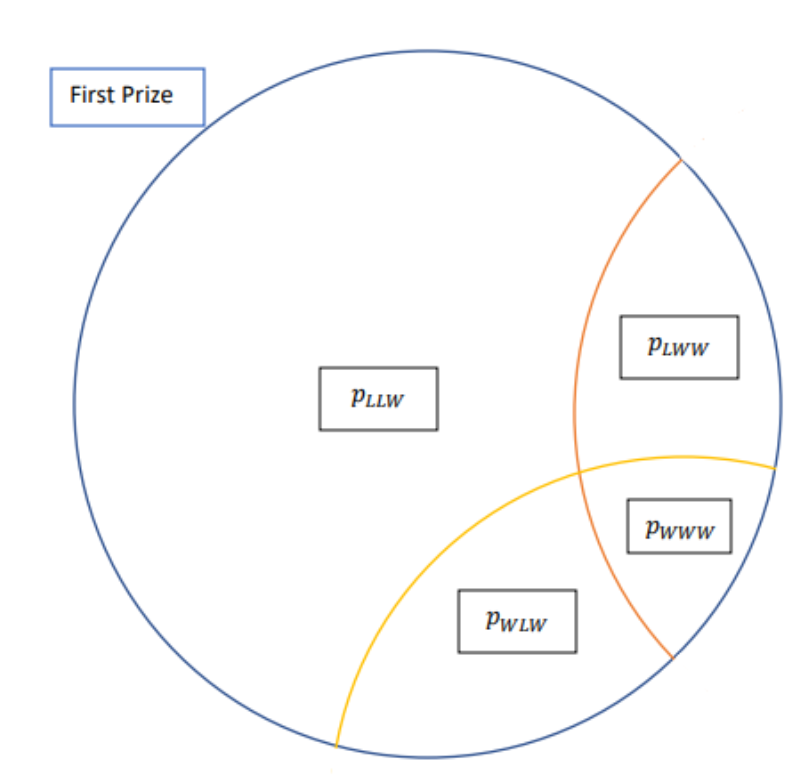
Looking at the first circle tells us that we can add the four probabilities to get the probability of winning the first prize.
![\[p_1 = P(\mbox{Winning First Prize}) = p_{LLW} + p_{LWW} + p_{WLW} + p_{WWW}\]](https://duddhawork.com/wp-content/ql-cache/quicklatex.com-8659e18e9a3f8e99fa091fb0dfdaac56_l3.png "Rendered by QuickLaTeX.com")
That said, the probability of winning the first prize and no other prizes would simply be 
. Using these probabilities, we can easily calculate the expected value for all possibilities.
We can now calculate the expected value for all number of tickets purchased.
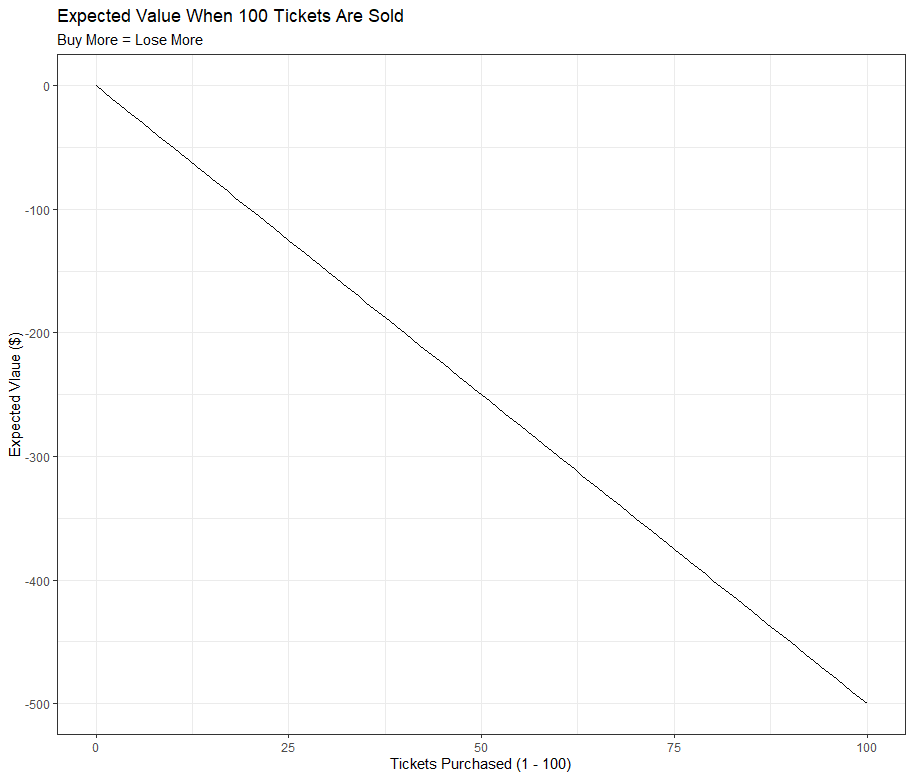
The graph above makes it clear that the more tickets we buy, the more we would lose in the long run. Buying all the 100 tickets does not make any sense either since you would pay $2000 to only win at $1500 worth of prizes (EV = -500 when n = 100 and N = 100). Each ticket purchased results in a decrease of five dollars to our expected value. The linear equation of our expected value is
![\[\mbox{EV}(n, N =100) = -5n + 0\]](https://duddhawork.com/wp-content/ql-cache/quicklatex.com-3cec22530b9cea1ae8ca4da97fb101b6_l3.png "Rendered by QuickLaTeX.com")
The answer to our initial question of how many tickets we should buy to maximize our expected value when 100 tickets are sold is ZERO. In other words, the best way to minimize your losses would be to not buy any tickets.
What is the maximum number of tickets that they can sell so we can have a chance of making money in the long term?
Tranlating this question mathematically: What is the greatest to that would result in the expected value to be greater than zero? Let’s consider what would happen to the expected value if they only sold 10 tickets? You can imagine that $20 is a cheap price to pay to have a 30% chance of winning a prize. We can also calculate the expected value of each number of tickets bought.
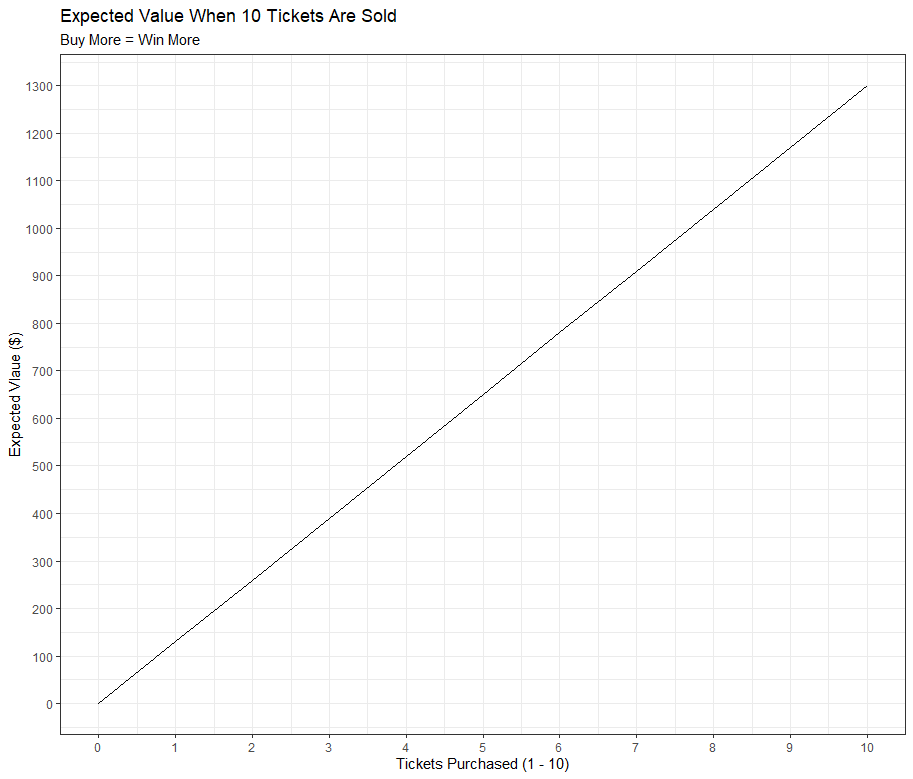
This time, the best way to maximize your expected value when 10 tickets are sold would be to buy all 10 tickets. It would cost you $200 but you would be guaranteed to win all three prizes for a total value of $1500. You can expect to win on average an extra $130 in the long run for every extra purchased ticket. The linear equation of our expected value is
![\[\mbox{EV}(n, N =10) = 130n + 0\]](https://duddhawork.com/wp-content/ql-cache/quicklatex.com-11d2fa97aa03feecbdab6a9877e56670_l3.png "Rendered by QuickLaTeX.com")
I built this Desmos calculator so that you can explore how the relationship between the expected value and the tickets sold and purchased.
It is worth noting from the visualization above that the number of tickets purchased does not change the slope of our expected value equation. The expected value is zero when they sell 75 tickets. Our EV is positive when they sell less than 75 tickets and negative when they sell more than 75 tickets. This should be somewhat intuitive since we know they start making money once they sell at least 75 tickets.
We can also display the tickets sold on the x-axis to show that the expected value becomes negative when they sell more than 75 tickets.
The visualization above confirms that the draw favors the couple when they sell more than 75 tickets. In terms of expected value, it does not make sense for us to buy tickets unless there are less than 75 tickets.
Can we plot the expected value in 3D?
The expected value depends on two variables. The number of tickets purchased and the number of tickets sold. We can plot this type of equation in 3D with GeoGebra to get a sense of how the variables interact. You can click on the Algebra calculator symbol to get rid of all the equations. You may also want to press twice on the minus sign to be able to see the axes. In red, we have the number of tickets purchased. In green, we have the number of tickets sold. In blue, we have the expected value in dollars. The fuzzy orange line represents when they sell 75 tickets.
We see that the expected value (the red curved surface) is positive when the number of tickets sold is less than 75.
Closing Thoughts
We found that our expected value becomes positive when the couple sells less than 75 tickets. Our expected value changes linearly for a fixed number of tickets sold. The initial EV is always zero when we do not buy any tickets. This implies that we should always buy more tickets if they sell less than 75 and always buy no tickets if they sell more than 75 if we only look at the expected value to make our decision.
There are many other factors worth taking into account when deciding how many tickets to buy. First, we often do not know how many tickets are going to be sold in advance. We can always try to estimate this value but it makes the pure expected value approach pretty limited. Second, it might not make sense to buy all 60 tickets if you knew they only printed 60. Sure, you would have profited an extra $300 (
). However, you almost certainly won’t be able to resell the smart TV and the cooler for their original retail value. This means that you may choose to keep the prizes instead. Is having a smart TV that is marginally better than your existing TV worth the price you paid for it? Maybe you needed the money to pay off some credit card debt. Maybe this $1200 came from your children’s education fund. It is important to differentiate between the value (dollars) and the utility (hapiness) of the same outcomes. For example, the YETI coolor is valued at $200 (high value) but has relatively low utility for you if you never go camping.
I like to gamble. Your expected value is much better for local fundraiser events such as this one compared to big government lotteries such as 649 or lotto max. I see these events as a great way to support my friends and causes I care about. The potentiality of winning something is just a bonus. You are guaranteed to win at the casino if you only bring approximately $50. If you lose it all, then you spent $50 for a great night. If you lose 
dollars then you only paid 
for a great night. If you break even, then you had a great night for free. If you made money, then you got paid to have fun with friends. The key is in determining what amount you are willing to pay to have a great night without thinking twice.
Oh and by the way, I did not win any prize with the one ticket I purchased. I guess I made the wrong decision;)