7 Basketball Shots as Spatial Objects
Note that all the R code used in this book is accessible on GitHub.
Let's load the basketball court and spatial polygons we've built in the previous chapters.
# Load the plot_court() function from the previous chapters
source("code/court_themes.R")
source("code/fiba_court_points.R")
# Load the different zone polygon objects
source("code/zone_polygons.R")
# Load libraries
library(tidyverse) # ggplot and dplyr
library(sf) Next, we can load the augmented basketball shots data set we created in Chapter 2.
# Load shot data
shots <- readRDS(file = "data/shots_augmented.rds")
# Display the first few rows
head(shots) %>% select(-shot_made_numeric, -dist_meters, -theta_rad)## # A tibble: 6 x 6
## player loc_x loc_y shot_made_factor dist_feet theta_deg
## <fct> <dbl> <dbl> <fct> <dbl> <dbl>
## 1 Player 7 4.39 7.96 Make 23.3 26.0
## 2 Player 3 5.78 8.51 Miss 23.4 13.9
## 3 Player 7 3.00 7.08 Make 23.3 39.2
## 4 Player 3 3.38 7.20 Miss 22.9 36.2
## 5 Player 13 3.16 7.20 Miss 23.3 37.6
## 6 Player 7 3.33 7.14 Miss 22.8 36.8Note that we have access to who took the shot, whether they made it or not, and from where on the court they released it. From there, we used the Pythagorean theorem to calculate the shot distance from the center of the hoop and we used trigonometric ratios to calculate the angle from the center line.
7.1 The Spatial Advantage
We can convert our augmented shot data to an sf object to take advantage of the spatial nature of the data.
# convert shots to an sf object
shots_sf <- st_as_sf(shots, coords = c("loc_x", "loc_y"))
# View sf object
shots_sf %>% select(-shot_made_numeric, -dist_meters, -theta_rad)## Simple feature collection with 1163 features and 4 fields
## Geometry type: POINT
## Dimension: XY
## Bounding box: xmin: 0.366552 ymin: 1.072896 xmax: 14.71044 ymax: 9.802368
## CRS: NA
## # A tibble: 1,163 x 5
## player shot_made_factor dist_feet theta_deg geometry
## <fct> <fct> <dbl> <dbl> <POINT>
## 1 Player 7 Make 23.3 26.0 (4.386864 7.95528)
## 2 Player 3 Miss 23.4 13.9 (5.7798 8.510016)
## 3 Player 7 Make 23.3 39.2 (3.003072 7.083552)
## 4 Player 3 Miss 22.9 36.2 (3.377976 7.202424)
## 5 Player 13 Miss 23.3 37.6 (3.161568 7.202424)
## 6 Player 7 Miss 22.8 36.8 (3.329208 7.141464)
## 7 Player 7 Make 2.01 82.2 (6.89232 1.658112)
## 8 Player 7 Make 23.2 39.4 (3.009168 7.050024)
## 9 Player 11 Make 23.3 38.8 (3.05184 7.10184)
## 10 Player 18 Miss 22.6 37.2 (3.344448 7.059168)
## # ... with 1,153 more rowsThe simple fact that our shots dataframe is now an sf object means that we can use the st_join() function which will automatically join create zone columns based on the location of each shot.
# shot_zone_range
shots_sf <- st_join(
x = shots_sf,
y = distance_polys
) %>%
# shot_zone_area
st_join(
y = angle_polys
) %>%
# shot_zone_basic
st_join(
y = basic_polys
) %>%
# area_value
st_join(
y = point_polys
) %>%
# shot_value
mutate(
shot_value = ifelse(area_value == "Two-Point Area", 2, 3)
) %>%
# Reorder and only keep relevant variables
select(player, shot_made_numeric, shot_made_factor,
dist_feet, dist_meters, theta_deg, theta_rad, shot_value,
shot_zone_range, shot_zone_area, shot_zone_basic, area_value,
geometry)The easiest way to test whether the join worked properly would be to randomly select a few shots and plot their different zone labels.
set.seed(123) # Always Display the same shots
sample_shots_sf <- shots_sf %>% slice_sample(n = 20)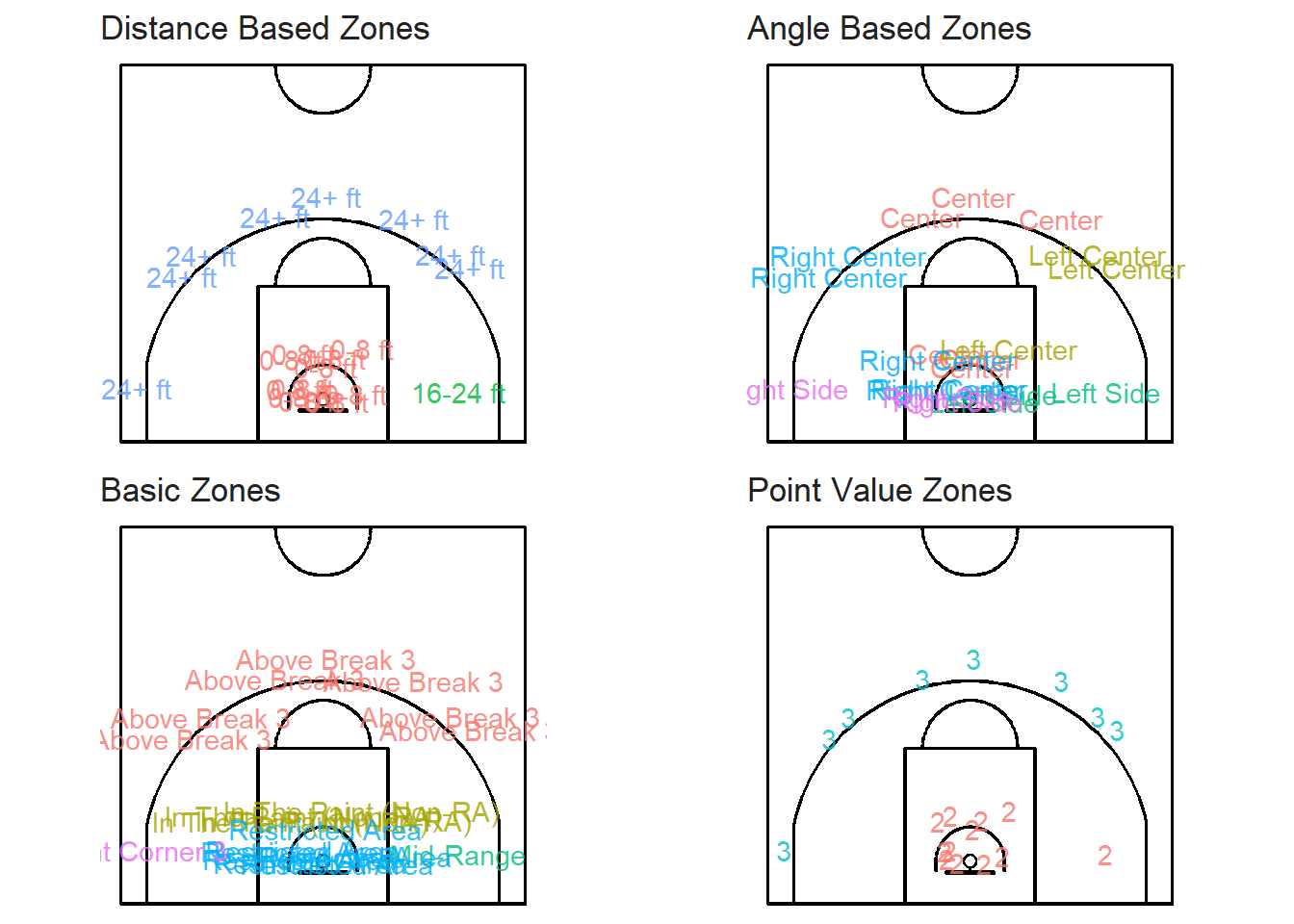
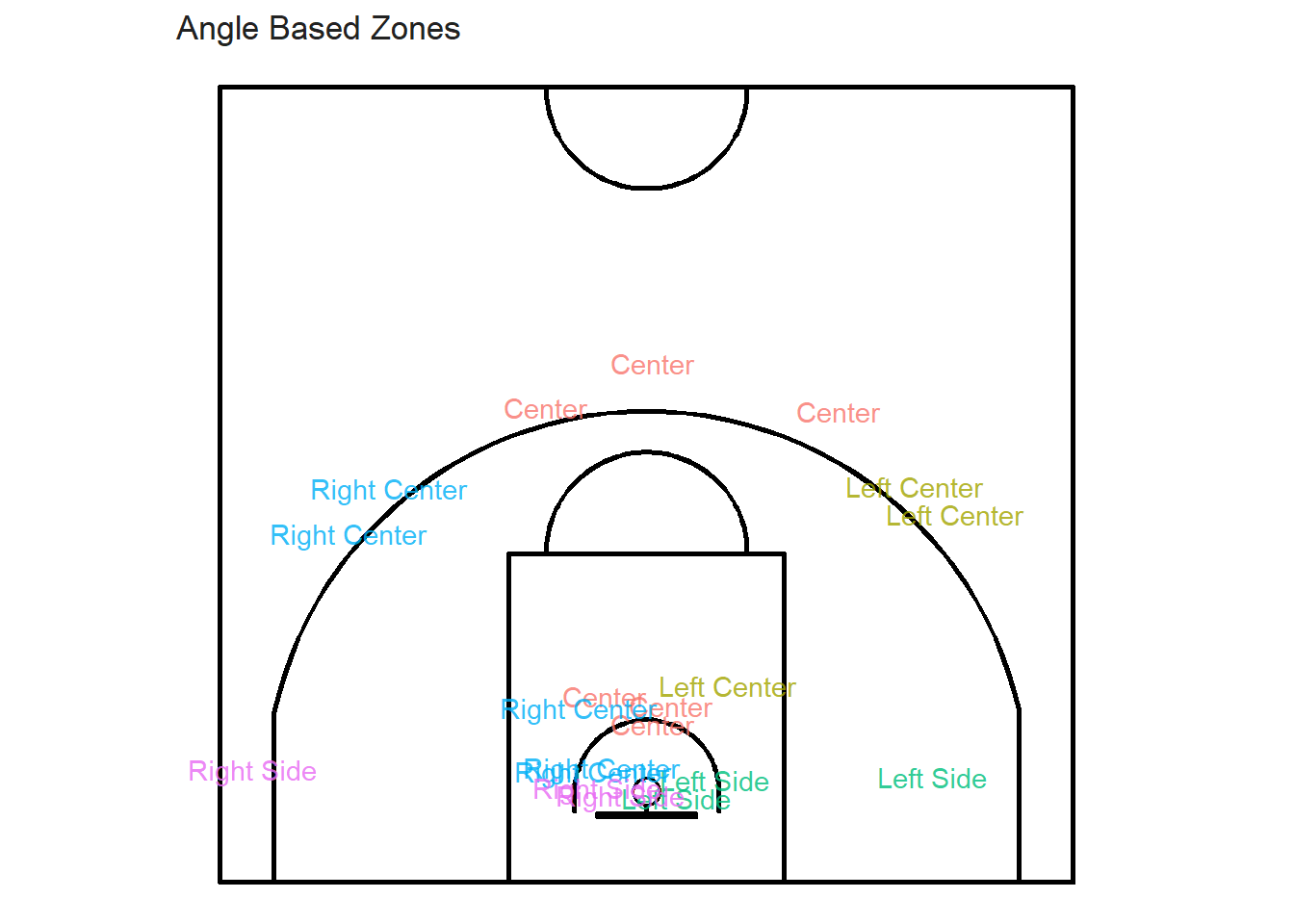
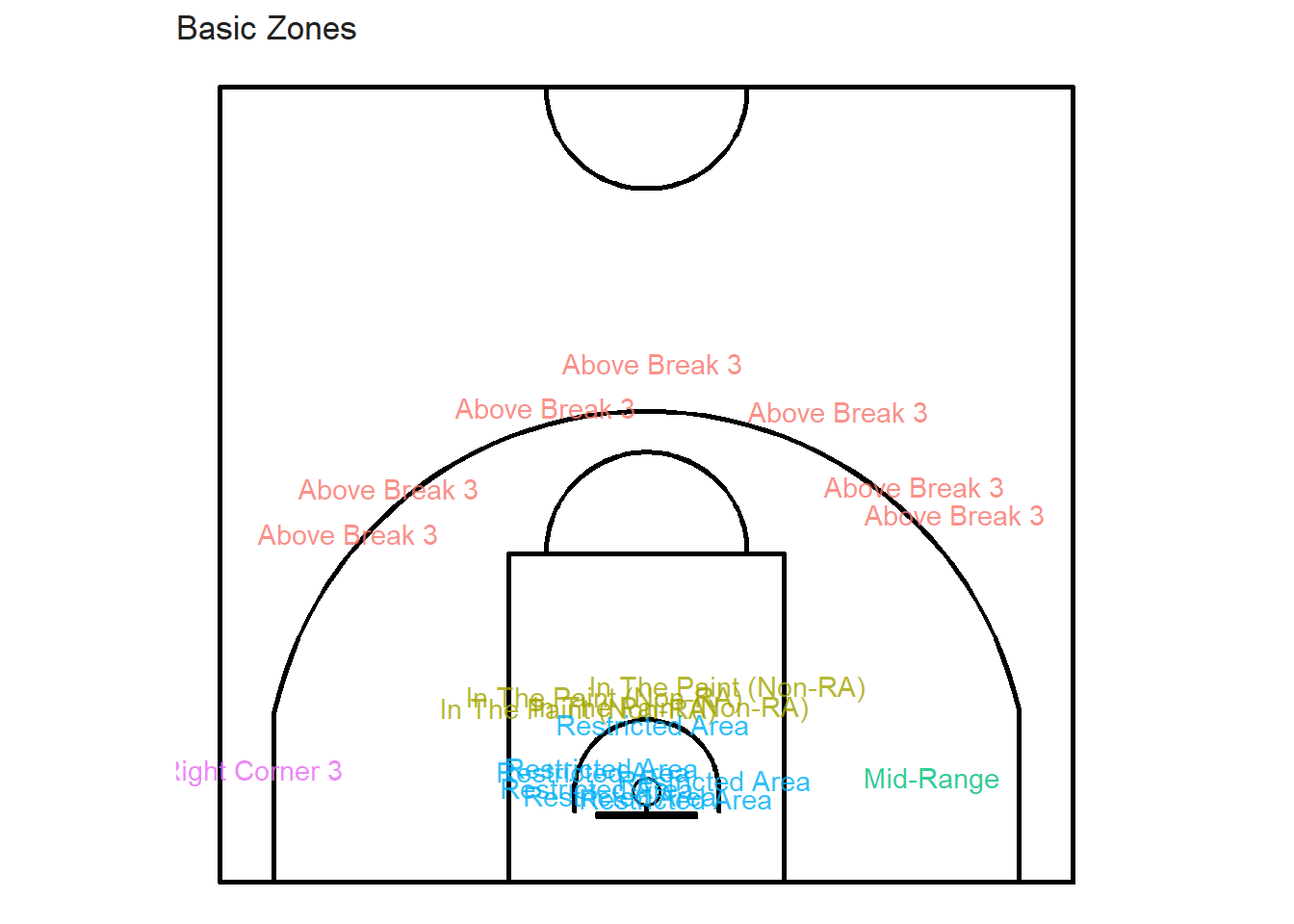
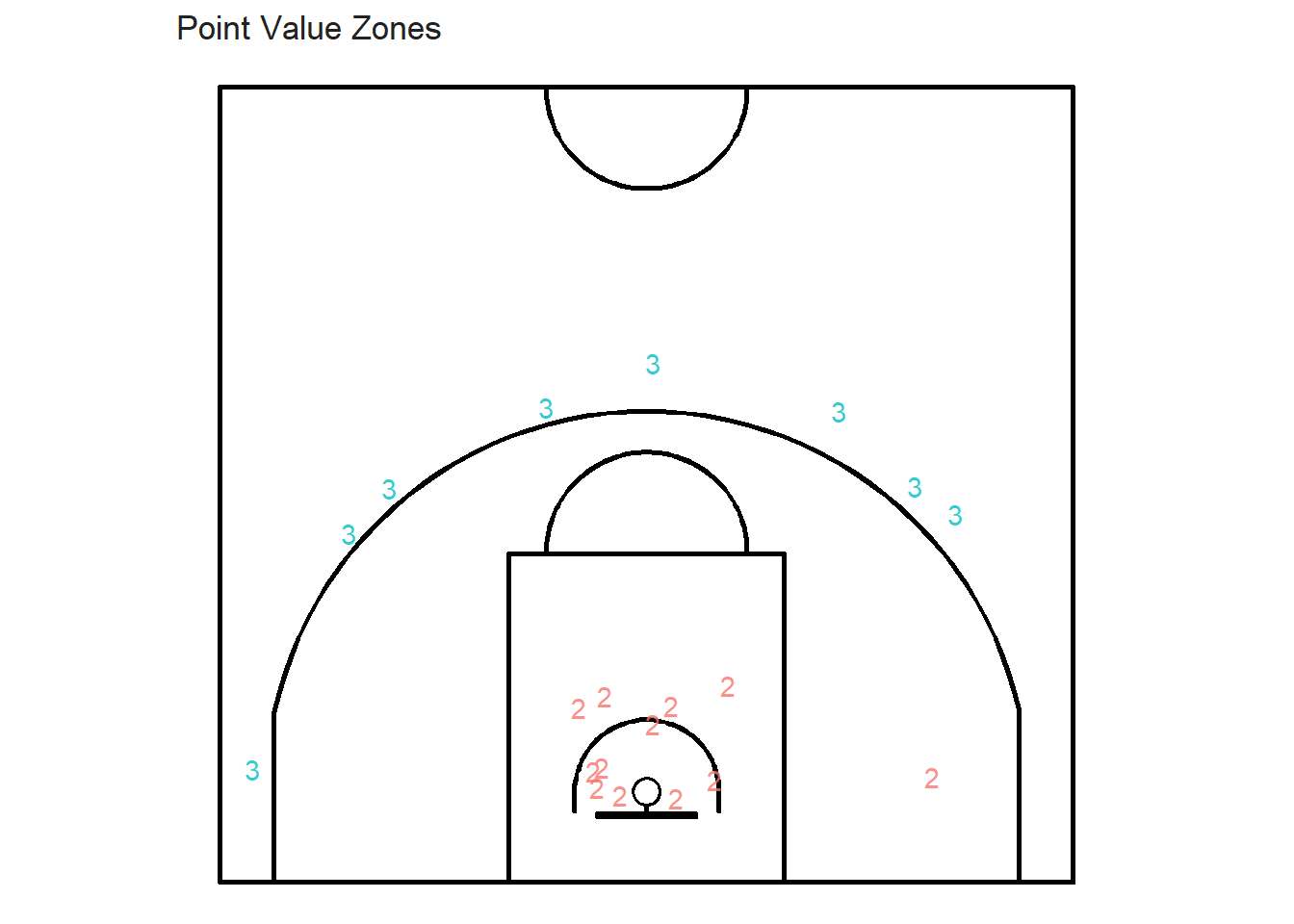
It seems like our joins worked properly. In the next chapter, we will create our first shot chart. How exciting! More specifically, we will try to determine whether the shot locations are spatially randomly distributed or if they seem to cluster.
Note that all the R code used in this book is accessible on GitHub.