6 Dividing the Court into Zones

Note that all the R code used in this book is accessible on GitHub.

There are many ways to split up a basketball court into zones. For this reasons, we will match the way that the NBA does it (see the Todd W. Schneider's BallR for more info).

6.1 Basic Zones

Let's create sf polygons for these zones to later conduct some spatial analysis. Creating these polygons is very similar to what we've done in the previous chapter so we'll focus on the zones themselves instead of focusing on the code.

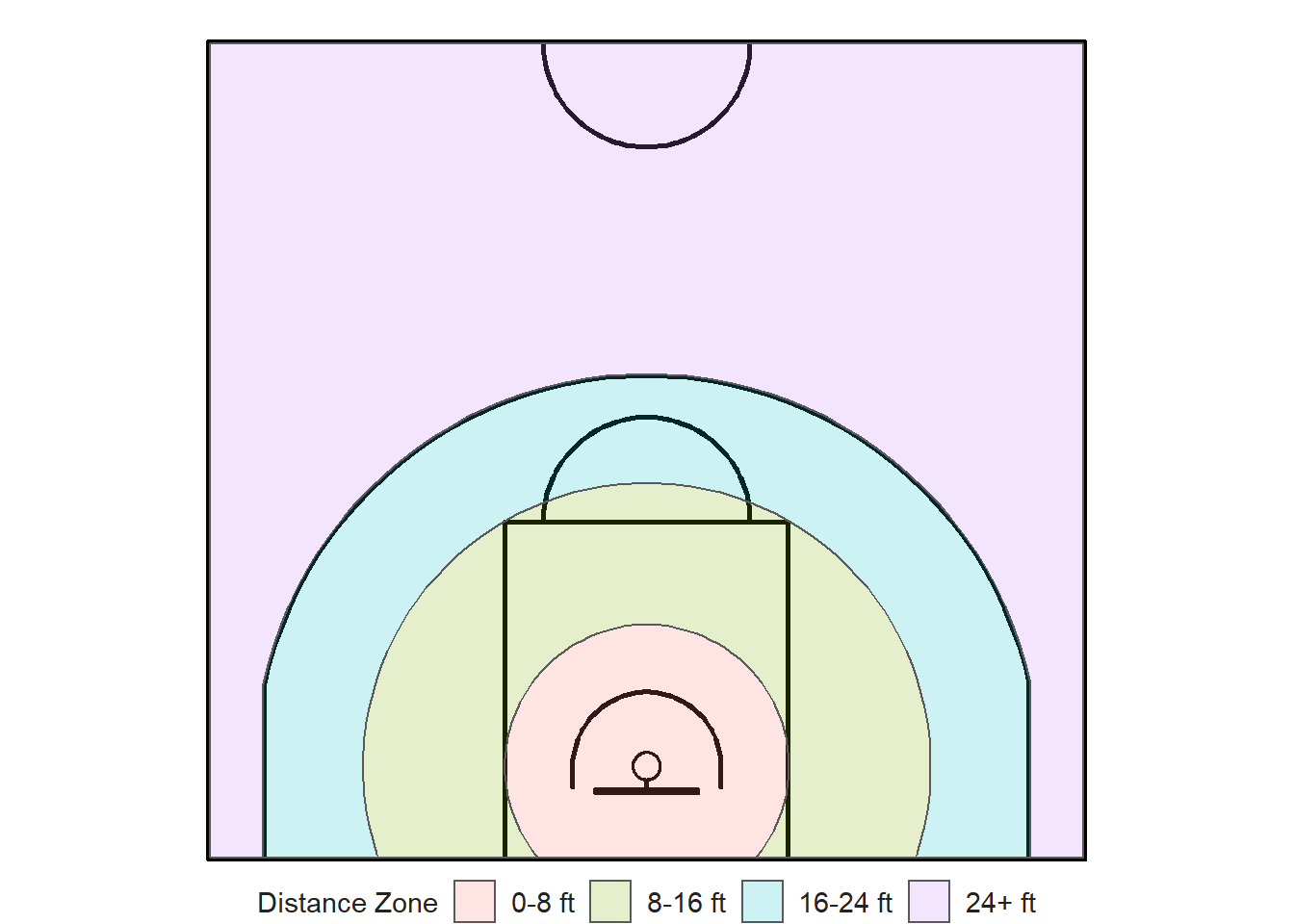
As you can see from the picture above, the basic zones are mutually exclusive and cover the entirety of the half-court. Thus, each shot could be assigned a basic zone using st_join(). From there, it is easy to calculate summary statistics for each zone.

6.2 Point Value

We can also create polygons for the two areas with different point values.

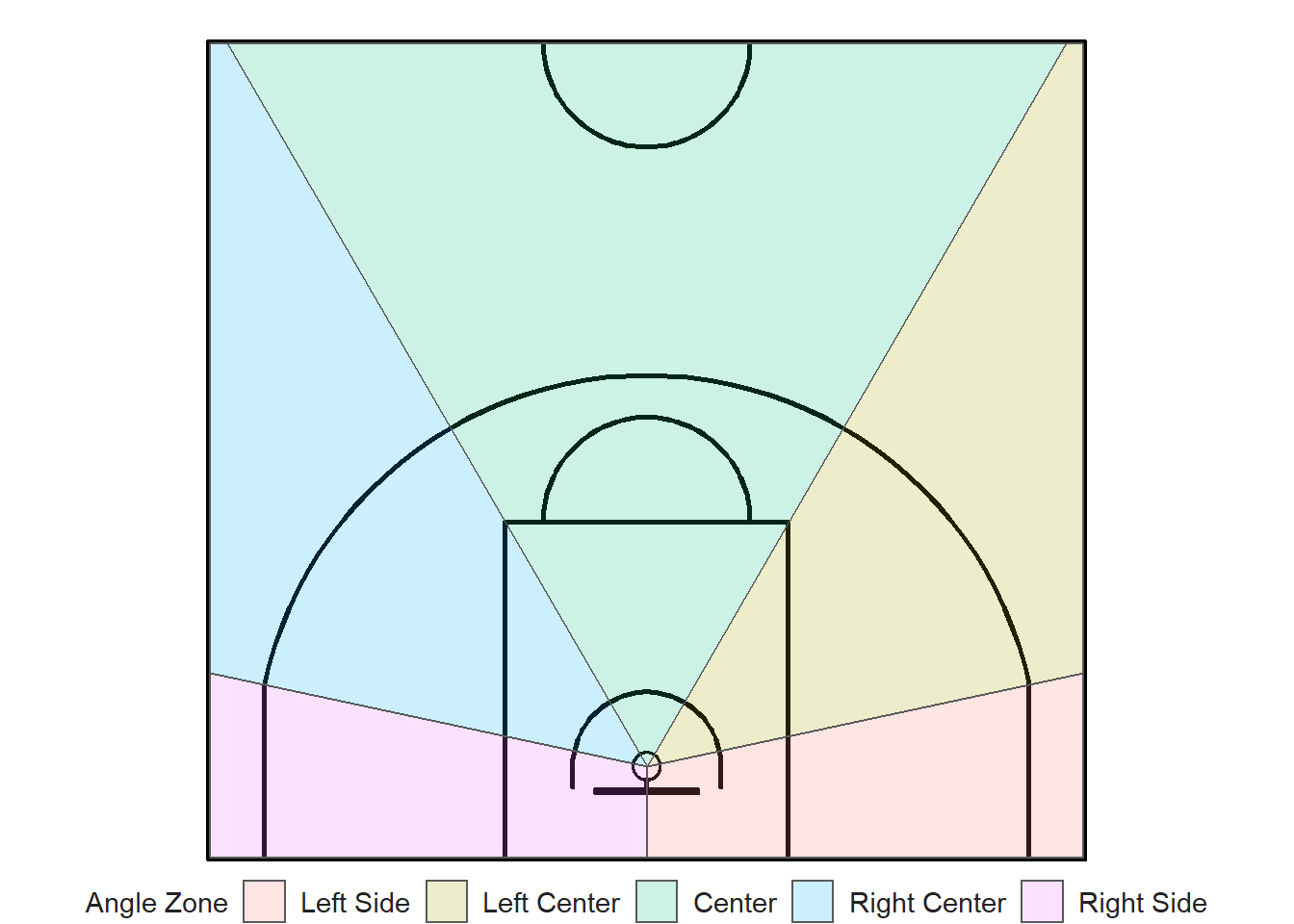This is useful since the three-point and two-point shot attempts are considered for the field goal percentage. Check out this extensive glossary of basketball statistics. Knowing the point-value of each shot is crucial to calculate the effective field goal percentage which adjusts for the fact that a 3-point field goal is worth one more point than a 2-point field goal.

6.3 Shot Distance

Next, we can separate the court into zones based on distance.

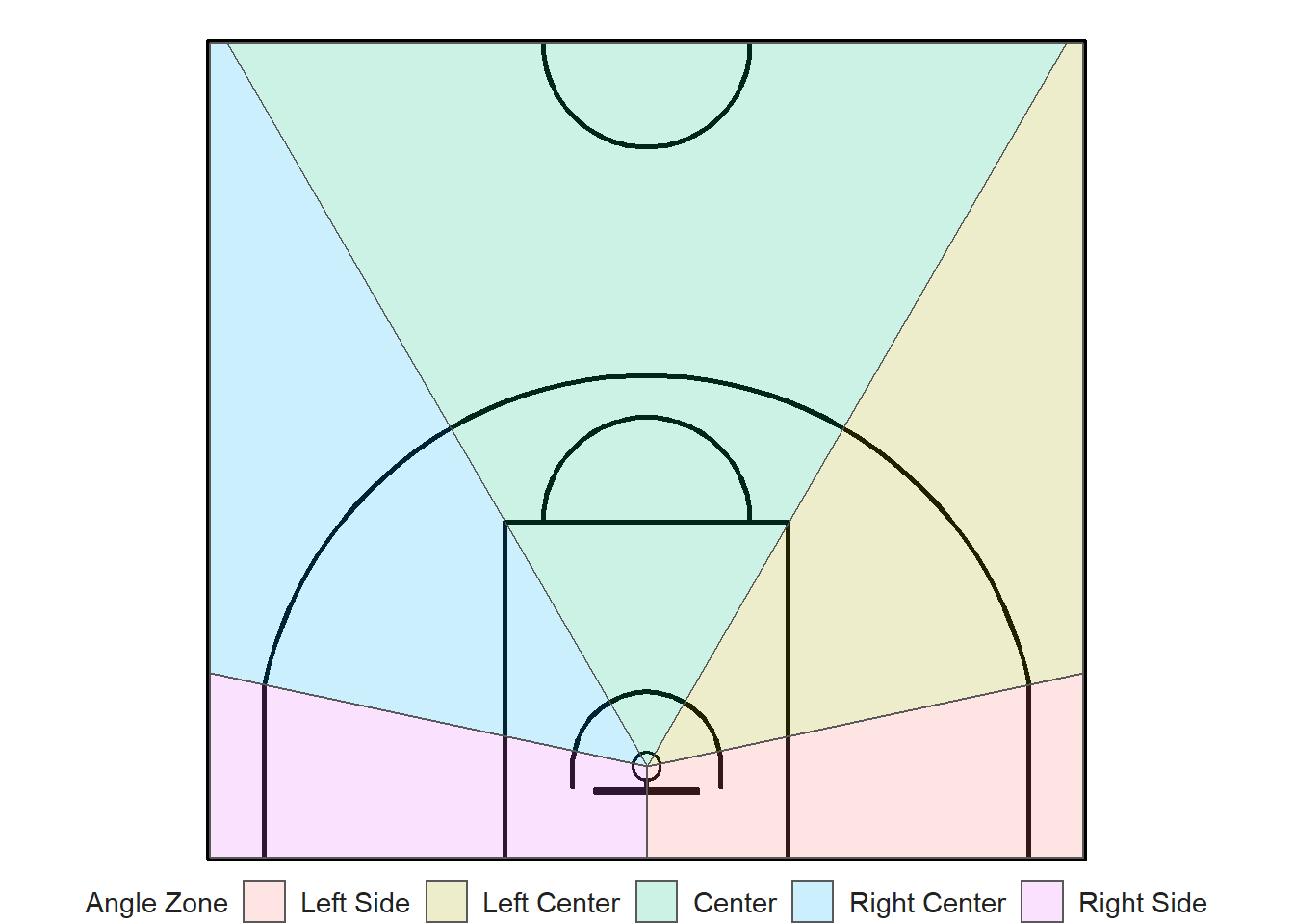We know that the distance from the hoop has a significant effect on the probability of making a shot. Being able to easily bin your shots by distance is crucial.

6.4 Shot Angle

Lastly, we can split the court by angle. We chose the line that goes through the center of the hoop and the exterior corner of the top key and the line that also goes through the center of the hoop but crosses the top exterior point of the straight part of the three-point line. Finding the \((x, ~y)\) coordinates of the red dots in the picture below can be challenging.

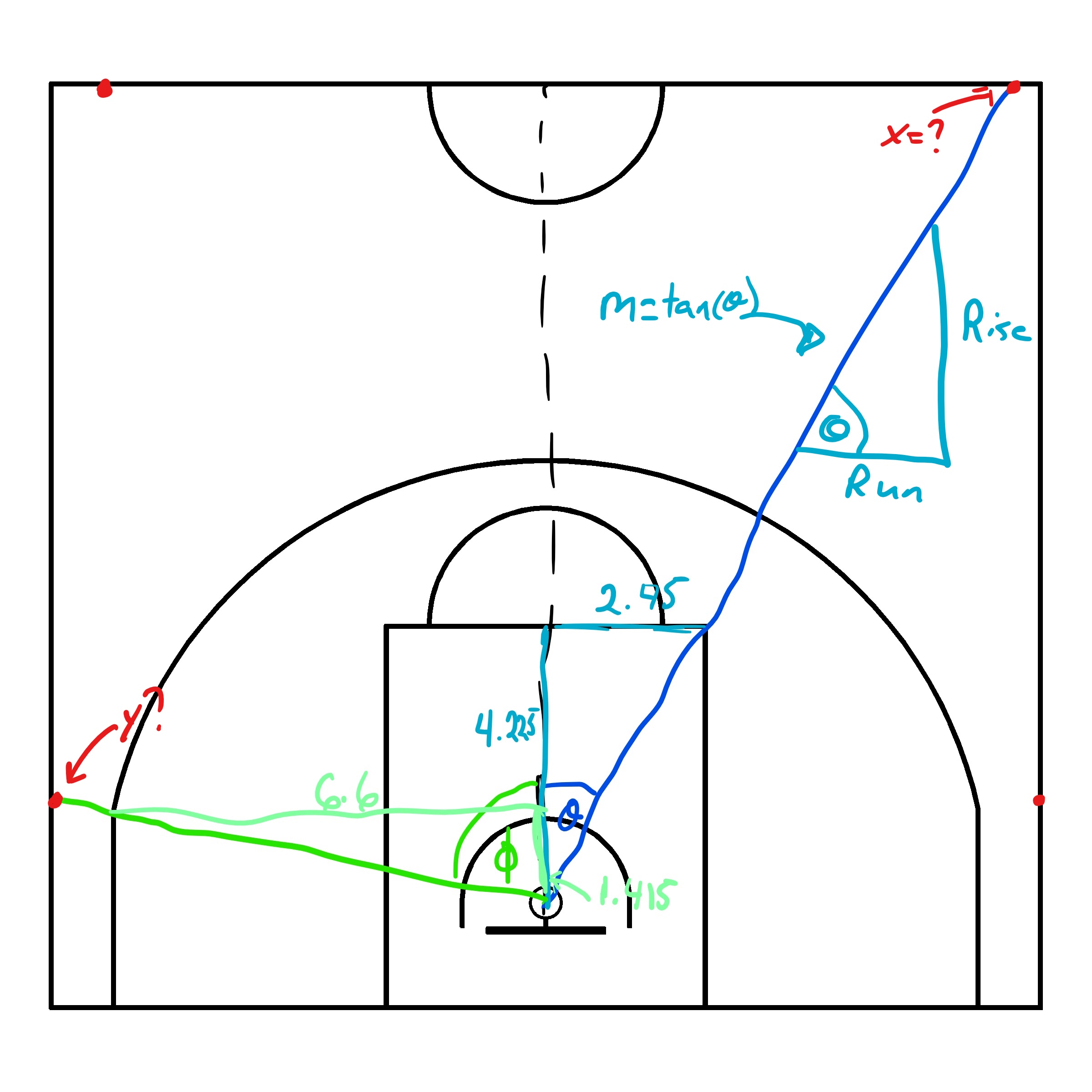
We can calculate \(\theta\) and \(\phi\) from the image by using SOH CAH TOA. Since we have the measures for the adjacent and opposite sides of each angles, we will use the tangent trigonometric ratio (TOA). We get that \(\theta = \arctan{\frac{O}{A}} \approx 30^{\circ}\) and \(\phi \approx 78^{\circ}\).

We know any line has equation \(y = mx + b\). We also know that once the slope of a line can be represented as \(tan(\theta)\) where \(\theta\) is the angle from the horizontal. That said, we have \(y = \tan{(\theta)}x + b\). We know that the center of the hoop lies on both lines so we can substitute \(x\) and \(y\) in each line equation with \((7.5, ~1.575)\) to solve for the y-intercepts \(b\). The coordinates of the red dots can now be easily identified once we know the line equations and one of their components.

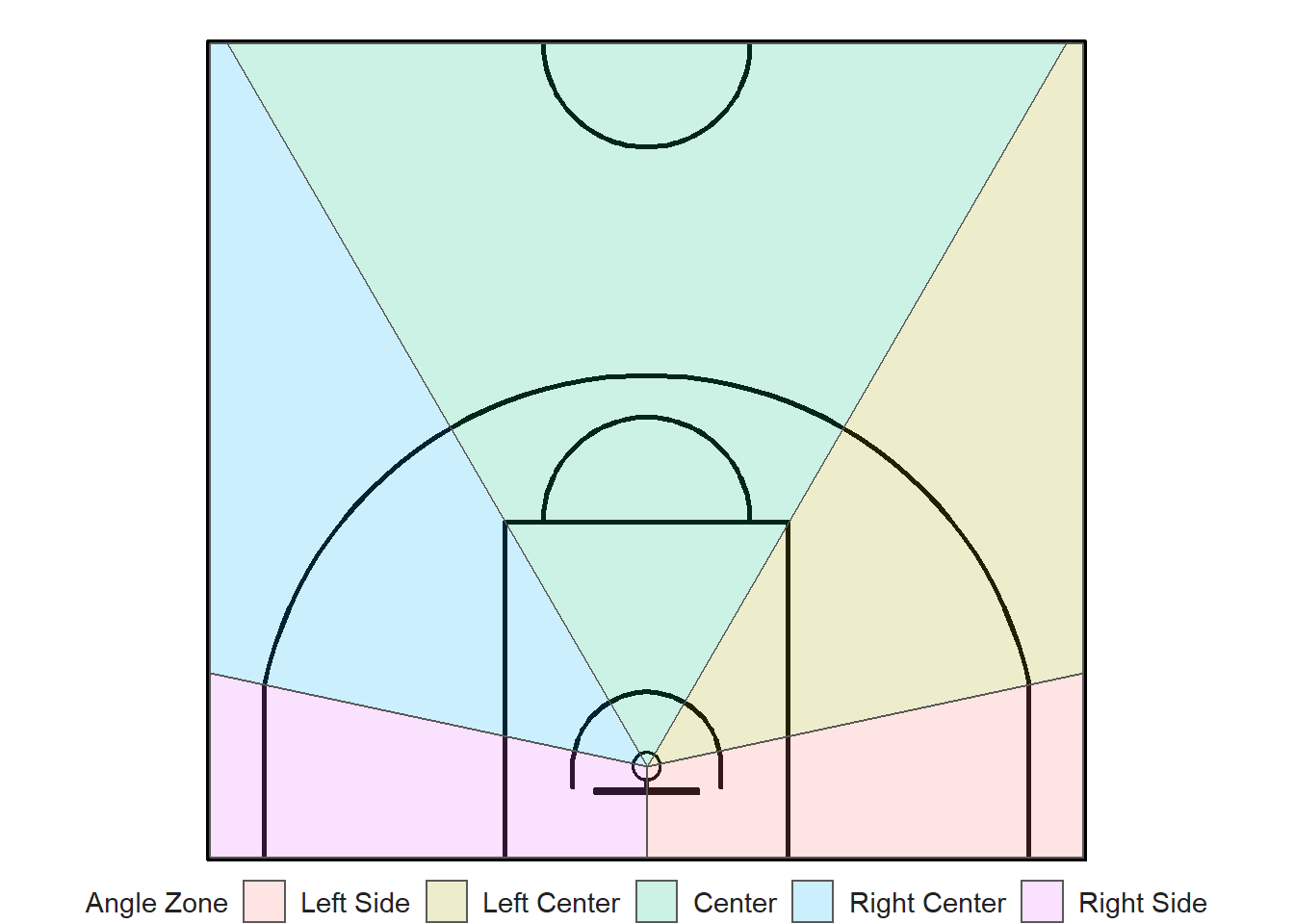
We will see in the next chapter how we can use these zone polygons to create an augmented spatial basketball shots data set.

Note that all the R code used in this book is accessible on GitHub.