3 Modeling Basketball Shots
Note that all the R code used in this book is accessible on GitHub.
Shot distance and shot angle can always be calculated given shot coordinates. Interesting insights can be generated from this augmented data. Let's try to get a better understanding of how these variables affect shooting percentage. Let's load the data we created in Chapter 2.
3.1 Visusalizing our Data
3.1.1 Shot Distance
We can try to visualize the relationship between shot distance15 and the probability of making a shot.
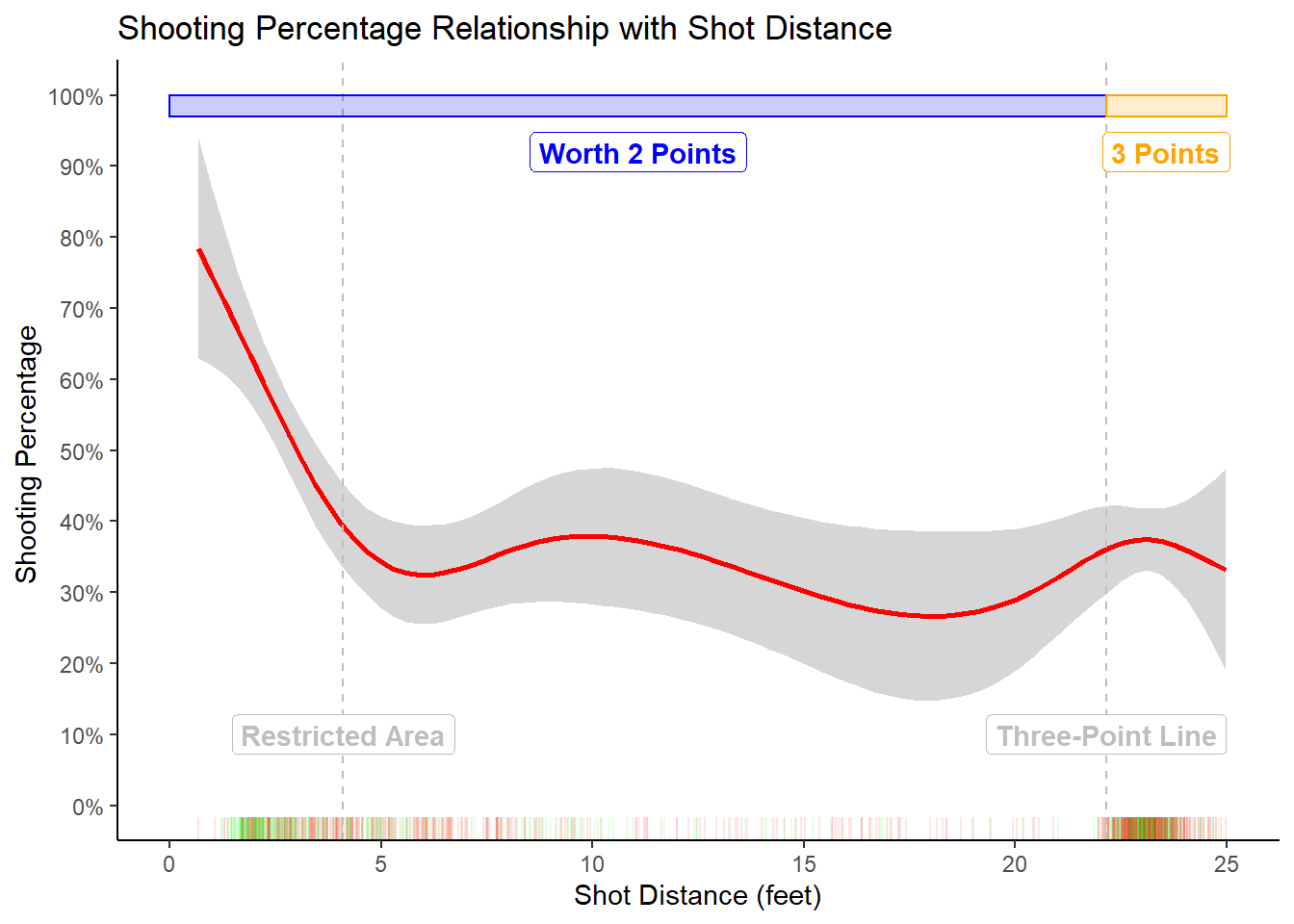
Figure 3.1: How distance affects shooting percentage
The accuracy starts off at approximately 75% for shots at the rim and levels off at 35% for shots further than 5 feet from the hoop. That's a drop in shooting percentage of roughly 40 percentage points within the first five feet! Notice that the three-point shooting percentage is not much different from the mid-range accuracy.
This plot provides evidence for the hypothesis proposed in Chapter 1. Attempts at the rim provide more expected points per shot than any other shot attempt. This is especially true considering that attackers tend to get fouled more often by attacking the rim.
An average team will make about 75% of their free throw attempts16. Three quarters of two points is 1.5 points which is even better than the expected points of layups sitting at \(0.6 \times 2 ~\mbox{points} = 1.2\) expected points per shot. Furthermore, the average mid-range shot from our sample produced roughly \(0.35 \times 2 ~\mbox{points} = 0.7\) points per shot compared to \(0.35 \times 3 ~\mbox{points} = 1.05\) points per shot for the average three-point attempt. This implies that teams who evaluate their possessions through the lens of expected points should embrace the following hierarchy for possession quality:
\[ \mbox{2 or more free throws} > \mbox{lay up} > \mbox{3-pointer} > \mbox{mid-range} \] Of course, this strategy needs more nuance. Its implementation will depend on many factors such as the score of the game, who is on the court, the time remaining on the clock, and so on. Nevertheless, teams at the highest levels of the game have found success by reorienting their strategy to mirror this framework17.
3.1.2 Shot Angle
We can also attempt to visualize how the angle from the center line of each shot affects shooting performance. Players often report that it is easier to shoot from the center of the court. Noah Basketball has also found that players taking three-point shots from the corners tended miss systematically away from the backboard18. This bias was stronger from the right-corner which was hypothesized to have something to do with the fact that most shooters are right-handed. Refer to Section 2.3.2 to see how we defined our shot angle reference system.
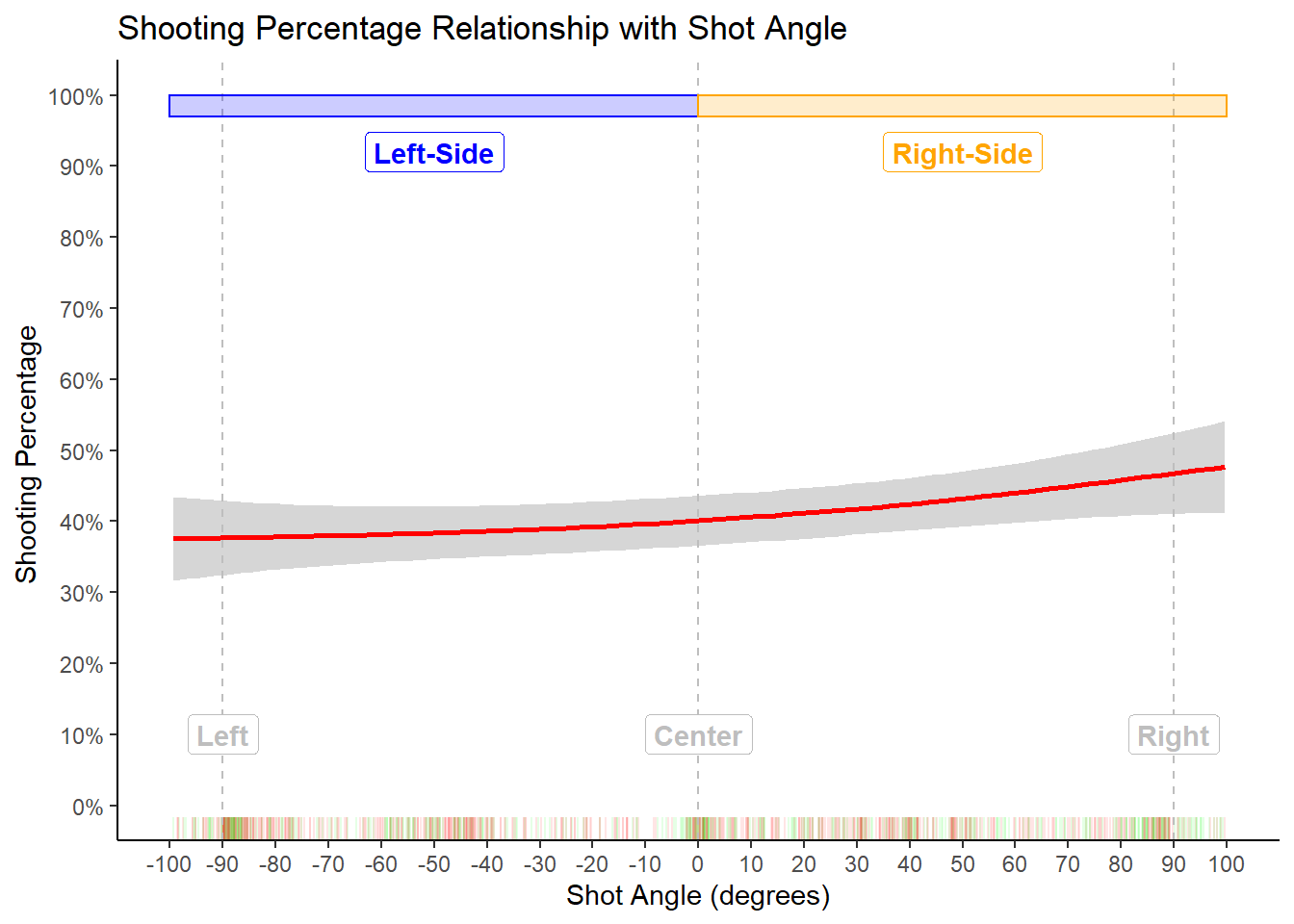
Figure 3.2: How angle affect shooting percentage
Shots coming from the center do not seem to go in at a significantly higher rate than shots coming from the sides. There appears to be slight increase in shooting percentage as shots move from the left side to the right side of the court. However, this effect may not be robust enough to be statistically or practically significant. The rug distribution of shots located at the bottom of the graph indicates clusters at \(0^{\circ}\), \(45^{\circ}\), and \(90^{\circ}\). This makes sense given common basketball offensive strategies.
Keep in mind that not all shots from \(90^{\circ}\) are created equal. It could be that right layups could in at a higher rate, but right corner shots go in at a lower rate. We could create separate pictures for each range of distance, but we'll see how we can control for shot distance with a statistical model19.
The previous plot showed no obvious large differences between shooting from the left or right side of the court. We can take the absolute value of the shooting angle to essentially fold our graph in half. This allows us to narrow in on the effect of shooting angle on shooting percentage instead without differentiating between the left and right side of the court.
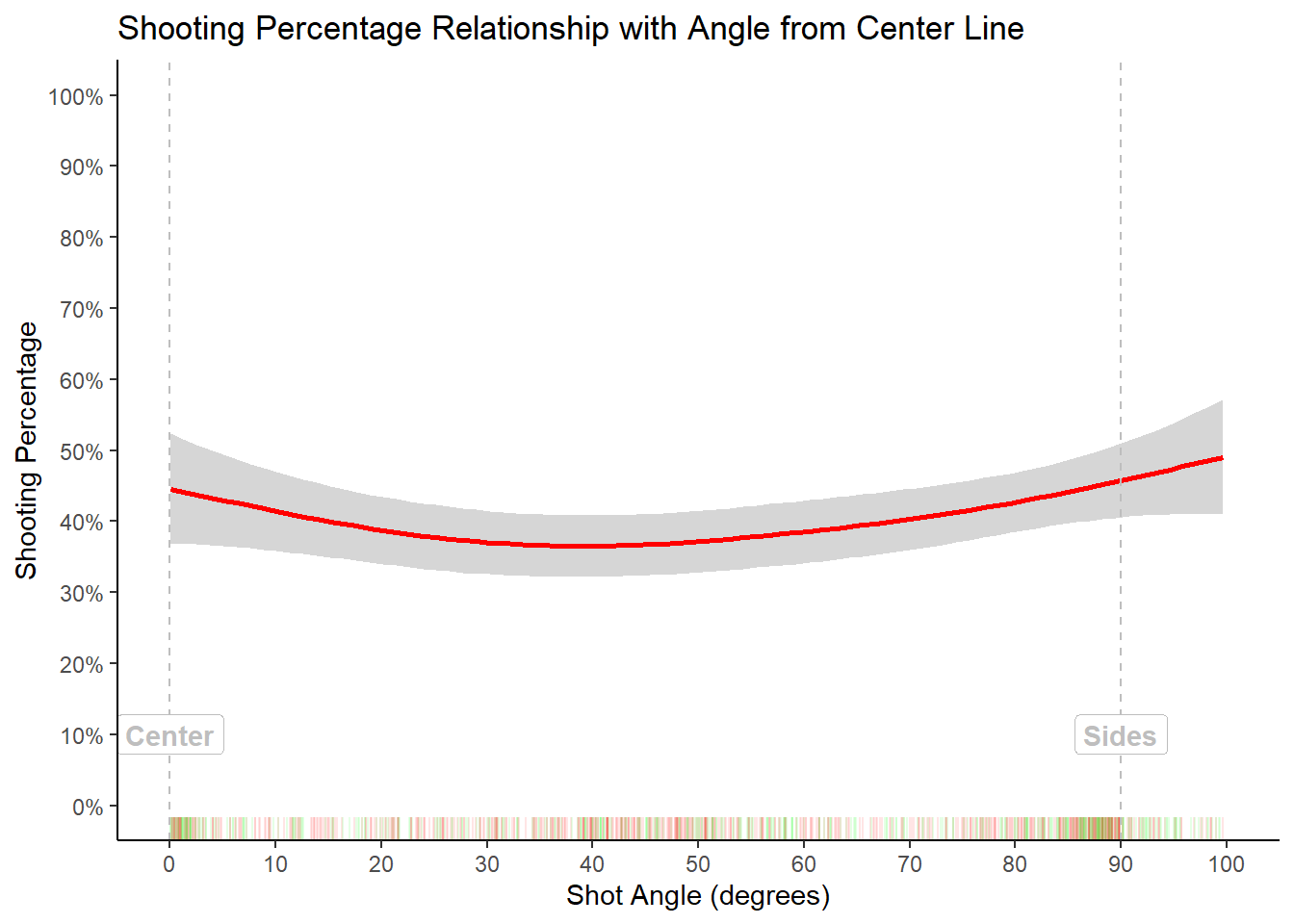
Figure 3.3: How the absolute value of the angle affects shooting percentage
Taking the absolute value of the shooting angle reveals a different story. Shooting from the sides and center (compared to shooting from \(45^{\circ}\)) seemed to result in greater accuracy. Again, this could be heavily biased by layups. The relationship between shot angle and accuracy is not clear cut for our sample. More data and modeling may shed more insight.
3.1.3 Player
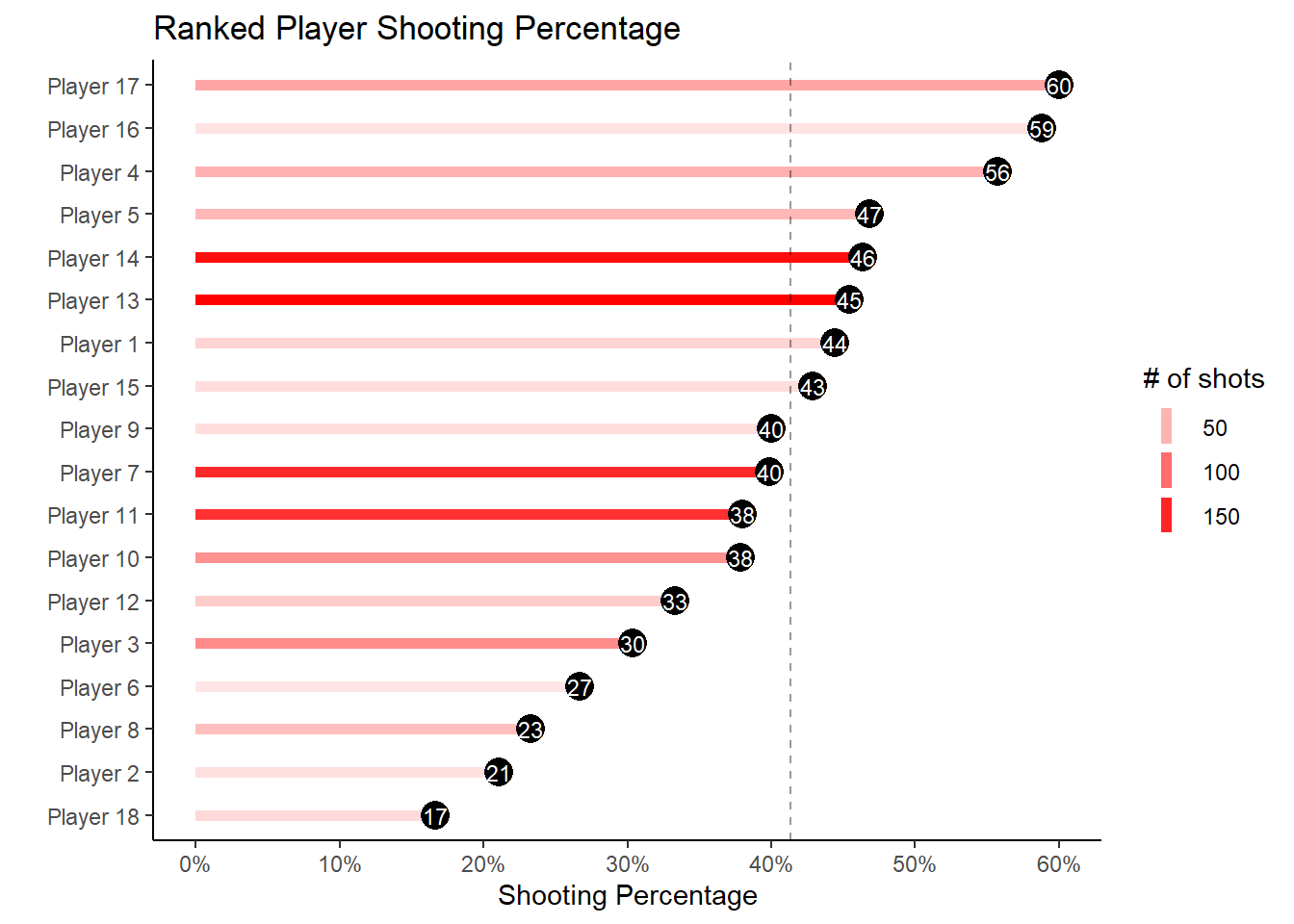
Figure 3.4: How the player affects shooting percentage
As you can see from Figure 3.4, some players shoot better than others. Strictly looking at the field goal percentages can be misleading however. What if the most accurate shooter only took easy layups? We will see how we can try to separate shot ability from shot difficulty by modeling our data below or in Chapter 13.
3.2 Quantifying these Effects
Pretty pictures are great. That said, they may struggle to display and quantify how different variables may interact. Technically, the red squiggle from geom_smooth() in the pictures above used a model20 to predict the accuracy of the shooters for every distance. Let's try to model these effects more thoroughly.
3.2.1 Logistic Regression
Logistic regression is a machine learning tool used to model binary outcomes (made or missed shot in our case). We won't dive too deep into the modeling rabbit hole since the focus of this book is on the spatial analysis of basketball shots with an emphasis on visualizations.
We are trying the find the average shooter's probability of making a shot given a certain distance (measured in feet). Mathematically speaking, we can write this probability as:
\[ P(X) = P(Y = \mbox{Make} ~| ~ X = \mbox{distance}) \] We know that probabilities have to range between zero and one. The issue with using the classic linear regression model21 is that a straight line can give values higher than one or lower than zero22. To keep our probabilities between zero and one, we can use the logistic function.
\[ P(X) = \frac{e^{\beta_0 + \beta_1X}}{e^{\beta_0 + \beta_1X} + 1} \]
Note that exponentiating \(\beta_0 + \beta_1X\) removes the possibility of a negative probability. We also divide a positive number by a a greater positive number to keep our output below 1 (hence the \(+1\) in the denominator).
The logistic function can be rearrange in the following way:
\[ \log \left( \frac{P(X)}{1 - P(X)} \right) = \beta_0 + \beta_1X \]
Note that we can easily switch back and forth between the log-odds23, the odds24, and the probability25 of making a shot given a specific distance once we calculated \(\beta_0\) and \(\beta_1\).
Let's fit some models in R using the glm() function with its family argument set to binomial to specify that we want a logistic regression model.
Note that all the R code used in this book is accessible on GitHub.
3.2.2 Distance Logistic Regression Model
# Fit a logistic regression model to predict the P(make|distance)
log_mod_dist <- glm(
formula = shot_made_numeric ~ dist_feet,
family = 'binomial', data = shots)| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | -0.012 | 0.104 | -0.119 | 0.905 |
| dist_feet | -0.025 | 0.006 | -3.886 | 0.000 |
We see that our distance variable is significant with a p-value of approximately 1 per 1000. The observed coefficient for the \(X\) is \(\beta_1 = -0.0249184\) which implies that the log-odds of making a shot (versus missing it) decrease by 0.0249184 for every extra foot further from the hoop. The previous sentence is very difficult to interpret. We usually think and talk in terms of odds and probabilities. We can also exponentiate \(\beta_1\) to interpret it as an odds-ratio26.
| odds_ratio | 2.5 % | 97.5 % | |
|---|---|---|---|
| (Intercept) | 0.988 | 0.805 | 1.212 |
| dist_feet | 0.975 | 0.963 | 0.988 |
The odds ratio for making a shot versus missing is 0.9753895. Let's take the reciprocal of this odds ratio so it is easier to interpret. We get \(\frac{1}{0.9753895} = 1.0252314\). This implies that the odds of missing a shot (versus making it) increase by 2.52% for every one foot increase in distance. We can also calculate the predicted probabilities of making the shot given the distance.
| shot_made_numeric | player | dist_feet | theta_deg | make_prob_dist |
|---|---|---|---|---|
| 0 | Player 10 | 22.865 | 49.027 | 0.358 |
| 1 | Player 13 | 1.558 | 97.649 | 0.487 |
| 1 | Player 14 | 24.825 | -0.822 | 0.347 |
| 0 | Player 17 | 1.741 | -101.506 | 0.486 |
| 0 | Player 5 | 3.993 | -80.302 | 0.472 |
| 0 | Player 13 | 24.068 | -48.038 | 0.352 |
| 0 | Player 11 | 7.776 | -37.337 | 0.449 |
| 0 | Player 8 | 22.863 | 86.658 | 0.358 |
| 0 | Player 3 | 5.184 | -15.625 | 0.465 |
| 0 | Player 2 | 16.549 | -86.977 | 0.395 |
We see that the model assigns a lower make probability for shots further away. In fact, we can visualize the relationship between the predicted probability of the model and shot distance. We will take advantage of this graph to illustrate the difference between a linear model and logistic model.
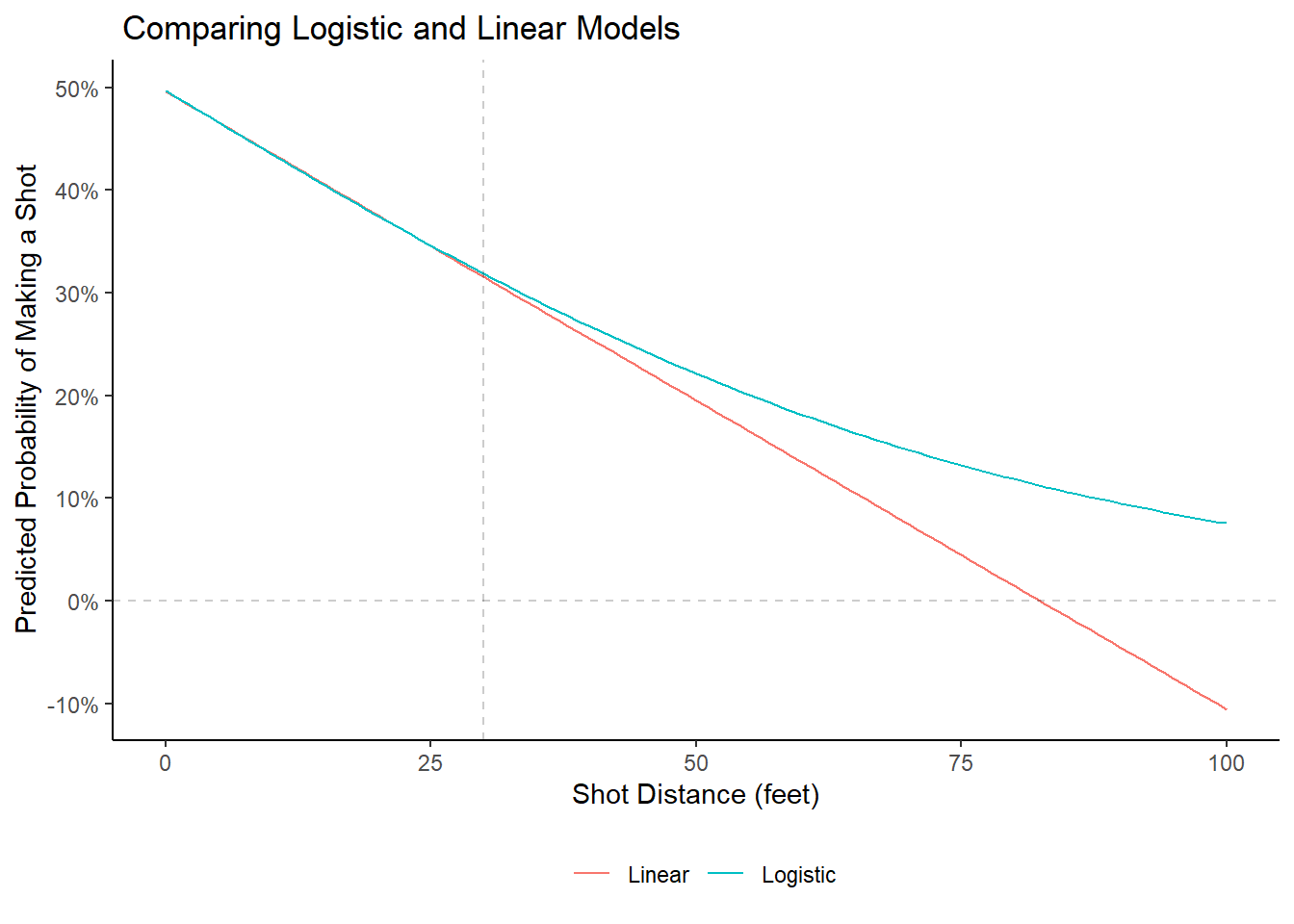
Figure 3.5: The linear model predicts negative probabilities
Of course, our shot data is limited to shots within about 30 feet of the rim. The plot was extended (up to 100 feet) to emphasize the difference between the two models. Both models predict essentially the same probability for making a shot for the first 30 feet. However, the linear model predicts negative probabilities for shots further than 80 feet or so. A probability can never be less than zero. This is why we go through the extra effort of working with the logistic regression.
Since the linear model is almost identical to the logistic model for the range of our data (0-30 feet), we can look at \(\beta_1\) for the linear regression model to see how an extra foot of distance affects the probability of making a shot. We have \(\beta_1 = -0.0060169\) . Player's are expected to lose approximately half a percent in their probability of making a shot for every extra foot of distance. Stated another way, the shooting percentage drops about 6% for every extra ten feet of distance. This makes sense since the predicted probability of making a shot at distance zero is roughly 0.5 and it is 0.32 at the 30 feet mark. This is a drop in predicted probability of 18% in 30 feet.
3.2.3 Angle Logistic Regression Model
# Fit a logistic regression model to predict the P(make|angle)
log_mod_theta <- glm(
formula = shot_made_numeric ~ abs(theta_deg),
family = 'binomial', data = shots)| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | -0.529 | 0.122 | -4.320 | 0.000 |
| abs(theta_deg) | 0.003 | 0.002 | 1.688 | 0.091 |
As expected from our exploratory plots, we see that the p-value for the angle coefficient is not significant at 5%. There was no clear relationship between the absolute value of the angle and the accuracy of the shooters. It wasn't like there was an obvious decrease or increase in accuracy as the players moved away from the center line.
The small but positive nature of the angle coefficient suggests that the log odds of making a shot slightly increase as you move away from the center. In other words, the model predicts a slight increase in shooting percentage when rotating away from the center line. This result could be tested experimentally but we can doubt this prediction given the magnitude and significance of the coefficient. Furthermore, the angle-only model does not control for distance and who's shooting the ball. We would intuitively expect the accuracy of players to be highest from the center. Additionally, there might be some left-right differences which weren't picked up by the model since we took the absolute value of the angle. More information is needed to make further inference.
3.2.4 Player Logistic Regression Model
We can also try to quantify the effect of who is shooting the ball on the probability of making a shot. Naturally, we can expect the shooter to have a significant impact on whether the shot is likely to go in or not. After all, the field goal percentages of the shooters varied greatly27.
# Fit a logistic regression model to predict the P(make|player)
log_mod_player <- glm(
formula = shot_made_numeric ~ player,
family = 'binomial', data = shots)| term | estimate | std.error | statistic | p.value |
|---|---|---|---|---|
| (Intercept) | -0.223 | 0.387 | -0.576 | 0.565 |
| playerPlayer 2 | -1.099 | 0.683 | -1.608 | 0.108 |
| playerPlayer 3 | -0.606 | 0.458 | -1.323 | 0.186 |
| playerPlayer 4 | 0.455 | 0.477 | 0.953 | 0.341 |
| playerPlayer 5 | 0.095 | 0.485 | 0.196 | 0.844 |
| playerPlayer 6 | -0.788 | 0.701 | -1.125 | 0.260 |
| playerPlayer 7 | -0.188 | 0.422 | -0.445 | 0.656 |
| playerPlayer 8 | -0.971 | 0.529 | -1.834 | 0.067 |
| playerPlayer 9 | -0.182 | 0.599 | -0.305 | 0.761 |
| playerPlayer 10 | -0.273 | 0.455 | -0.600 | 0.548 |
| playerPlayer 11 | -0.265 | 0.424 | -0.625 | 0.532 |
| playerPlayer 12 | -0.470 | 0.535 | -0.878 | 0.380 |
| playerPlayer 13 | 0.041 | 0.416 | 0.098 | 0.922 |
| playerPlayer 14 | 0.078 | 0.417 | 0.188 | 0.851 |
| playerPlayer 15 | -0.065 | 0.587 | -0.110 | 0.912 |
| playerPlayer 16 | 0.580 | 0.627 | 0.925 | 0.355 |
| playerPlayer 17 | 0.629 | 0.468 | 1.342 | 0.180 |
| playerPlayer 18 | -1.386 | 0.671 | -2.067 | 0.039 |
Notice how the intercept coefficient is set to Player 1 by default. As a result, all players are compared to Player 1. This just happens to be relevant since Player 1's field goal percentage is 44.44% which is close to the team average of 41.36%. In other words, the model is comparing each player's shooting percentage to roughly the team average. The only statistically significant coefficient is for Player 18. This is not surprising considering the dismal 16.67 shooting percentage of Player 18.
We can fit a logistic model with no intercept to get the log odds of each player to make a shot. Once that's done, we can easily convert the log odds into odds and probabilities.
# The +0 is to remove the intercept
player_no_int <- glm(
formula = shot_made_numeric ~ player + 0,
family = 'binomial', data = shots) %>%
tidy() %>%
# Calculate the log odds, odds, and probabilities
transmute(
player = substring(term, 7),
log_odds = estimate,
odds = exp(log_odds),
make_prob = odds / (1 + odds)
)| player | log_odds | odds | make_prob |
|---|---|---|---|
| Player 1 | -0.223 | 0.800 | 0.444 |
| Player 2 | -1.322 | 0.267 | 0.211 |
| Player 3 | -0.829 | 0.436 | 0.304 |
| Player 4 | 0.232 | 1.261 | 0.558 |
| Player 5 | -0.128 | 0.880 | 0.468 |
| Player 6 | -1.012 | 0.364 | 0.267 |
| Player 7 | -0.411 | 0.663 | 0.399 |
| Player 8 | -1.194 | 0.303 | 0.233 |
| Player 9 | -0.405 | 0.667 | 0.400 |
| Player 10 | -0.496 | 0.609 | 0.378 |
| Player 11 | -0.488 | 0.614 | 0.380 |
| Player 12 | -0.693 | 0.500 | 0.333 |
| Player 13 | -0.182 | 0.833 | 0.455 |
| Player 14 | -0.145 | 0.865 | 0.464 |
| Player 15 | -0.288 | 0.750 | 0.429 |
| Player 16 | 0.357 | 1.429 | 0.588 |
| Player 17 | 0.405 | 1.500 | 0.600 |
| Player 18 | -1.609 | 0.200 | 0.167 |
Note that the predicted make_prob column is identical to the field goal percentage of each player28. The model is essentially using field goal percentages to predict whether a shot will go in or not. Of course, the technique is not ideal since not all shots are created equal. Maybe the player with low shooting percentages have been taking some tough three pointers and vice versa. Using strictly their field goal percentage to predict their probability of making a layup is obviously a flawed approach.
3.2.5 The Full Model
Let's try to create a full model to try to predict the probability of making a shot given:
- Shot distance
- Angle relative to the center of the court
- Player who took the shot
##
## Call:
## glm(formula = shot_made_numeric ~ dist_feet + theta_deg + player +
## 0, family = "binomial", data = shots)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.4320 -1.0430 -0.8056 1.2616 1.9945
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## dist_feet -0.024717 0.007742 -3.193 0.00141 **
## theta_deg 0.001784 0.001021 1.748 0.08051 .
## playerPlayer 1 -0.112976 0.390403 -0.289 0.77229
## playerPlayer 2 -1.198489 0.567170 -2.113 0.03459 *
## playerPlayer 3 -0.608828 0.256300 -2.375 0.01753 *
## playerPlayer 4 0.384707 0.283601 1.357 0.17494
## playerPlayer 5 0.225292 0.310151 0.726 0.46760
## playerPlayer 6 -0.598452 0.596688 -1.003 0.31588
## playerPlayer 7 -0.030622 0.204563 -0.150 0.88101
## playerPlayer 8 -0.600019 0.400173 -1.499 0.13377
## playerPlayer 9 -0.197254 0.461457 -0.427 0.66905
## playerPlayer 10 -0.306944 0.249914 -1.228 0.21937
## playerPlayer 11 -0.075098 0.212681 -0.353 0.72401
## playerPlayer 12 -0.357033 0.385394 -0.926 0.35423
## playerPlayer 13 0.226527 0.203341 1.114 0.26527
## playerPlayer 14 0.292551 0.206556 1.416 0.15668
## playerPlayer 15 0.319131 0.474453 0.673 0.50118
## playerPlayer 16 0.412564 0.496118 0.832 0.40564
## playerPlayer 17 0.491539 0.266352 1.845 0.06497 .
## playerPlayer 18 -1.124337 0.566803 -1.984 0.04730 *
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 1612.3 on 1163 degrees of freedom
## Residual deviance: 1520.9 on 1143 degrees of freedom
## AIC: 1560.9
##
## Number of Fisher Scoring iterations: 4Let's try to interpret some of these coefficients. As expected, the distance coefficient is significant and the log odds of making a shot decrease by 0.0247172 for every additional foot away from the basket. This effect is almost identical to the effect observed earlier for the distance-only logistic regression model29.
The same is true for the angle coefficient. It very similar to the coefficent of the angle-only model. It is not significant at 5% but is significant at 10%.
Now let's look at the estimates for the players. We see that some players have negative coefficients30 while others have positive coefficients. We can sort the players by their predicted probability of making a shot to get a better understanding of their coefficients.
| player | log_odds | odds | make_prob | real_fg | diff | p_value | significant |
|---|---|---|---|---|---|---|---|
| Player 17 | 0.492 | 1.635 | 0.620 | 0.600 | 0.020 | 0.065 | FALSE |
| Player 16 | 0.413 | 1.511 | 0.602 | 0.588 | 0.013 | 0.406 | FALSE |
| Player 4 | 0.385 | 1.469 | 0.595 | 0.558 | 0.037 | 0.175 | FALSE |
| Player 15 | 0.319 | 1.376 | 0.579 | 0.429 | 0.151 | 0.501 | FALSE |
| Player 14 | 0.293 | 1.340 | 0.573 | 0.464 | 0.109 | 0.157 | FALSE |
| Player 13 | 0.227 | 1.254 | 0.556 | 0.455 | 0.102 | 0.265 | FALSE |
| Player 5 | 0.225 | 1.253 | 0.556 | 0.468 | 0.088 | 0.468 | FALSE |
| Player 7 | -0.031 | 0.970 | 0.492 | 0.399 | 0.094 | 0.881 | FALSE |
| Player 11 | -0.075 | 0.928 | 0.481 | 0.380 | 0.101 | 0.724 | FALSE |
| Player 1 | -0.113 | 0.893 | 0.472 | 0.444 | 0.027 | 0.772 | FALSE |
| Player 9 | -0.197 | 0.821 | 0.451 | 0.400 | 0.051 | 0.669 | FALSE |
| Player 10 | -0.307 | 0.736 | 0.424 | 0.378 | 0.045 | 0.219 | FALSE |
| Player 12 | -0.357 | 0.700 | 0.412 | 0.333 | 0.078 | 0.354 | FALSE |
| Player 6 | -0.598 | 0.550 | 0.355 | 0.267 | 0.088 | 0.316 | FALSE |
| Player 8 | -0.600 | 0.549 | 0.354 | 0.233 | 0.122 | 0.134 | FALSE |
| Player 3 | -0.609 | 0.544 | 0.352 | 0.304 | 0.049 | 0.018 | TRUE |
| Player 18 | -1.124 | 0.325 | 0.245 | 0.167 | 0.079 | 0.047 | TRUE |
| Player 2 | -1.198 | 0.302 | 0.232 | 0.211 | 0.021 | 0.035 | TRUE |
We see that players with a predicted probability of a made shot above 50% have positive coefficients. Another interesting thing to note is that the predicted probability of making a shot for a specific player is not the same as their overall field goal percentage. This was the case for the angle-only logistic regression model31. In fact the predicted probabilities are consistently higher than the actual field goal percentages. This makes sense since the full model is trying to isolate the player's shooting ability independent of the location of their shots while the player-only model only considered the name of the player and not where they were shooting from.
The only players with significant coefficients are Player 3, Player 18, and Player 2. This implies that these players are shooting worse than the others independent of where they're shooting from. Player 17's coefficient is almost significant at 5% which gives us some evidence that they are shooting better than others independent of shot location.Some honorable mentions in terms of significance could go to Player 4 (good), Player 14(good), and Player 8 (bad).
Take a look at the bottom two rows of Table3.7. It is worth noting that the model predicted Player 2 to be a worse shooter than Player 18 although Player 2 had a higher field goal percentage32. The reason for this becomes evident once we compare their shot charts.
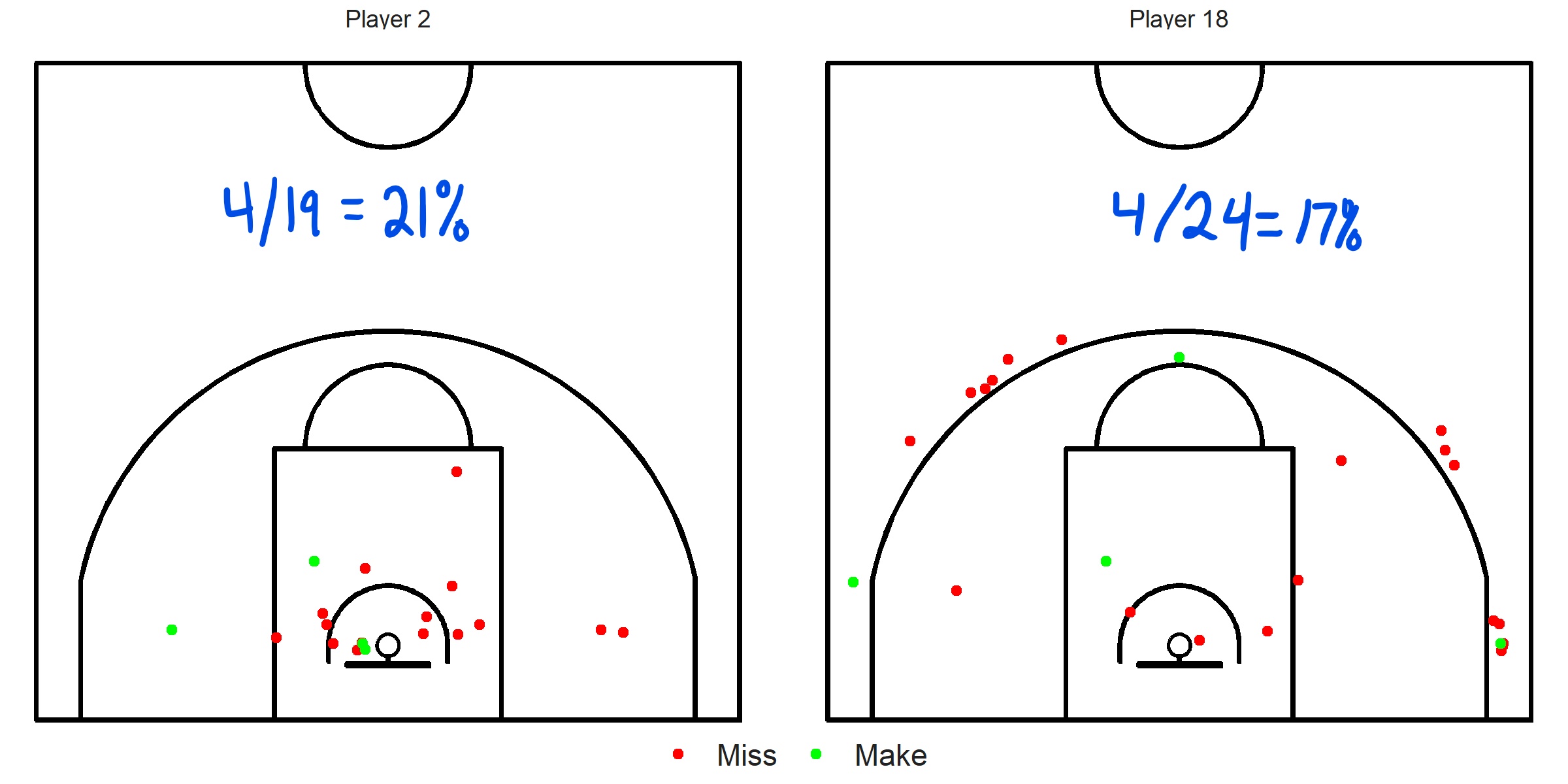
Player 18 is taking harder shots than Player 2. Therefore, when controlling for distance and angle, the model predicts that Player 18 is better shooter despite the lower field goal percentage.
| player | dist_feet | theta_deg | make_prob_dist | make_prob_full | outcome |
|---|---|---|---|---|---|
| Player 10 | 22.865 | 49.027 | 0.358 | 0.313 | 0 |
| Player 13 | 1.558 | 97.649 | 0.487 | 0.590 | 1 |
| Player 14 | 24.825 | -0.822 | 0.347 | 0.420 | 1 |
| Player 17 | 1.741 | -101.506 | 0.486 | 0.566 | 0 |
| Player 5 | 3.993 | -80.302 | 0.472 | 0.496 | 0 |
| Player 13 | 24.068 | -48.038 | 0.352 | 0.388 | 0 |
| Player 11 | 7.776 | -37.337 | 0.449 | 0.417 | 0 |
| Player 8 | 22.863 | 86.658 | 0.358 | 0.267 | 0 |
| Player 3 | 5.184 | -15.625 | 0.465 | 0.318 | 0 |
| Player 2 | 16.549 | -86.977 | 0.395 | 0.146 | 0 |
Lastly, Table 3.8 compares the predictions of the distance-only model to the predictions of the full model. We can see that the full model has some predictions which are over 50% which isn't the case for the distance model. In row 2 and 4, the distance model assigns a probability of 48% to both player of making the lay up while the full model gives the edge to Player 13 over Player 17.
3.3 Closing Thoughts
We barely scratched the surface of what is possible to do when modeling basketball shots. The aim of this chapter was twofold. First, it was meant to serve as an introduction to the key ideas and techniques of statistical modeling. Second, this chapter was designed to build some intuition about what constitutes a "good" shot attempt in basketball. This intuition will be vital to carry out the spatial analysis in the coming chapters.
The next chapter will explore how we can use the predicted probabilities from our logistic regression models to try to predict whether shots will go in or not.
Note that all the R code used in this book is accessible on GitHub.